题目内容
14.等差数列{an}的前n项和为Sn,且a3+a5=a4+7,S10=100.(1)求{an}的通项公式;
(2)求满足不等式Sn<3an-2的n的值.
分析 (1)由a3+a5=a4+7,S10=100,列出方程组,求出首项和公差,由此能求出{an}的通项公式.
(2)由a1=1,an=2n-1,求出Sn=n2,从而得到n2-6n+5<0,由此能求出n的值.
解答 (本题10分)
解:(1)设数列{an}的公差为d,
由a3+a5=a4+7,得2a1+6d=a1+3d+7,①.…(1分)
由S10=100,得10a1+45d=100,②…(2分)
解得a1=1,d=2,…(4分)
所以an=a1+(n-1)d=2n-1.…(5分)
(2)因为a1=1,an=2n-1,所以${S}_{n}=\frac{n({a}_{1}+{a}_{n})}{2}$=n2,…(7分)
由不等式Sn<3an-2,得n2<3(2n-1)-2,
所以,n2-6n+5<0,
解得1<n<5,…(9分)
因为n∈N*,
所以n的值为2,3,4.…(10分)
点评 本题考查等差数列的通项公式、项数n的求法,是基础题,解题时要认真审题,注意等差数列的性质的合理运用.

练习册系列答案
相关题目
6.己知x、y∈R,i是虚数单位,若x+yi与$\frac{2+i}{1+i}$互为共轭复数,则x+y=( )
| A. | -2 | B. | -1 | C. | 1 | D. | 2 |
3.执行如图所示的程序框图,如果输人的x=-10.则输出的y=( )


| A. | 0 | B. | 1 | C. | 8 | D. | 27 |
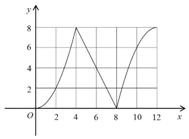 如图,函数f(x)的图象经过(0,0),(4,8),(8,0),(12,8)四个点,试用“>,=,<”填空:
如图,函数f(x)的图象经过(0,0),(4,8),(8,0),(12,8)四个点,试用“>,=,<”填空: