题目内容
9.设实数a,b,c满足a2+b2+c2=1.(Ⅰ)证明:ab+bc+ac≤1;
(Ⅱ)若$\sqrt{2}$a+$\sqrt{3}$b+2c≤|x-1|+|x+m|对任意的实数a,b,c,x恒成立,求实数m的取值范围.
分析 (Ⅰ)利用基本不等式可得a2+b2≥2ab,b2+c2≥2bc,c2+a2≥2ca,三式相加即得结论.由
(Ⅱ)柯西不等式,我们易结合a2+b2+c2=1,得到$\sqrt{2}$a+$\sqrt{3}$b+2c≤3,再由$\sqrt{2}$a+$\sqrt{3}$b+2c≤|x-1|+|x+m|对任意的实数a,b,c,x恒成立,得到3≤|x-1|+|x+m|,进而解绝对值不等式,即可得到答案.
解答 (Ⅰ)证明:由a2+b2≥2ab,b2+c2≥2bc,c2+a2≥2ca,
三式相加即得a2+b2+c2≥ab+bc+ca,又a2+b2+c2=1,
所以ab+bc+ca≤1.
(Ⅱ)解:∵($\sqrt{2}$a+$\sqrt{3}$b+2c)2≤(2+3+4)(a2+b2+c2)=9
∴$\sqrt{2}$a+$\sqrt{3}$b+2c≤3
又∵$\sqrt{2}$a+$\sqrt{3}$b+2c≤|x-1|+|x+m|对任意的实数a,b,c,x恒成立,
∴3≤|x-1|+|x+m|,
∵|x-1|+|x+m|≥|m+1|,
∴|m+1|≥3
解得m≤-4或m≥2.
点评 本题考查不等式的证明,考查基本不等式的运用,考查柯西不等式、绝对值不等式求解,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
20.函数f(x)=x2+cosx的导数f′(x)为( )
| A. | x-sinx | B. | 2x-sinx | C. | x+sinx | D. | 2x+sinx |
17.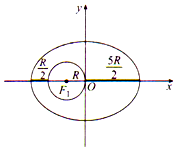 我国自主研制的第一个月球探测器--“嫦娥一号”卫星在西昌卫星发射中心成功发射后,在地球轨道上经历3次调相轨道变轨,奔向月球,进入月球轨道,“嫦娥一号”轨道是以地心为一个焦点的椭圆,设地球半径为R,卫星近地点,远地点离地面的距离分别是$\frac{R}{2}$,$\frac{5R}{2}$(如图所示),则“嫦娥一号”卫星轨道的离心率为( )
我国自主研制的第一个月球探测器--“嫦娥一号”卫星在西昌卫星发射中心成功发射后,在地球轨道上经历3次调相轨道变轨,奔向月球,进入月球轨道,“嫦娥一号”轨道是以地心为一个焦点的椭圆,设地球半径为R,卫星近地点,远地点离地面的距离分别是$\frac{R}{2}$,$\frac{5R}{2}$(如图所示),则“嫦娥一号”卫星轨道的离心率为( )
 我国自主研制的第一个月球探测器--“嫦娥一号”卫星在西昌卫星发射中心成功发射后,在地球轨道上经历3次调相轨道变轨,奔向月球,进入月球轨道,“嫦娥一号”轨道是以地心为一个焦点的椭圆,设地球半径为R,卫星近地点,远地点离地面的距离分别是$\frac{R}{2}$,$\frac{5R}{2}$(如图所示),则“嫦娥一号”卫星轨道的离心率为( )
我国自主研制的第一个月球探测器--“嫦娥一号”卫星在西昌卫星发射中心成功发射后,在地球轨道上经历3次调相轨道变轨,奔向月球,进入月球轨道,“嫦娥一号”轨道是以地心为一个焦点的椭圆,设地球半径为R,卫星近地点,远地点离地面的距离分别是$\frac{R}{2}$,$\frac{5R}{2}$(如图所示),则“嫦娥一号”卫星轨道的离心率为( )| A. | $\frac{2}{5}$ | B. | $\frac{1}{5}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{3}$ |
19.设a=($\frac{3}{4}$)0.5,b=($\frac{4}{3}$)0.4,c=log${\;}_{\frac{3}{4}}$(log34),则( )
| A. | a<b<c | B. | a<c<b | C. | c<a<b | D. | c<b<a |