题目内容
 某幼儿园小班的美术课上,老师带领小朋友们用水彩笔为美术本上如右图所示的两个大小不同的气球涂色,要求一个气球只涂一种颜色,两个气球分别涂不同的颜色.该班的小朋友牛牛现可用的有暖色系水彩笔红色、橙色各一支,冷色系水彩笔绿色,蓝色,紫色各一支.
某幼儿园小班的美术课上,老师带领小朋友们用水彩笔为美术本上如右图所示的两个大小不同的气球涂色,要求一个气球只涂一种颜色,两个气球分别涂不同的颜色.该班的小朋友牛牛现可用的有暖色系水彩笔红色、橙色各一支,冷色系水彩笔绿色,蓝色,紫色各一支.(1)牛牛从他可用的五支水彩笔中随机的取出两支按老师要求为气球涂色,问两个气球同为冷色的概率是多大?
(2)一般情况下,老师发出开始指令到涂色活动全部结束需要10分钟.牛牛至少需要2分钟完成该项任务.老师在发出开始指令1分钟后随时可能来到牛牛身边查看涂色情况.问当老师来到牛牛身边时牛牛已经完成任务的概率是多大?
考点:几何概型,古典概型及其概率计算公式
专题:概率与统计
分析:(1)由题意得到两个气球共20种涂色方案,其中有6种全冷色方案,由此能求出两个气球同为冷色的概率.(2)老师发出开始指令起计时,设牛牛完成任务的时刻为x,老师来到牛牛身边检查情况的时刻为y,利用几何概率能求出当老师来到牛牛身边时牛牛已经完成任务的概率.
解答:
解:(1)由题意得到如下表格:
∴两个气球共20种涂色方案,…(2分)
其中有6种全冷色方案,…(4分)
∴两个气球同为冷色的概率为
=
.…(6分)
(2)老师发出开始指令起计时,设牛牛完成任务的时刻为x,
老师来到牛牛身边检查情况的时刻为y,
则由题有
…式1,
若当老师来到牛牛身边时牛牛已经完成任务,
则
…式2,
如图所示,所求概率为几何概率
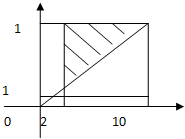 (10分)
(10分)
阴影部分(式2)面积为
•(10-2)•(10-2)=32
可行域(式1)面积为(10-1)•(10-2)=72
∴当老师来到牛牛身边时牛牛已经完成任务的概率为
=
.(12分)
| 红色 | 橙色 | 绿色 | 蓝色 | 紫色 | |
| 红色 | 0 | 1 | 1 | 1 | 1 |
| 橙色 | 1 | 0 | 1 | 1 | 1 |
| 绿色 | 1 | 1 | 0 | 2 | 2 |
| 蓝色 | 1 | 1 | 2 | 0 | 2 |
| 紫色 | 1 | 1 | 2 | 2 | 0 |
其中有6种全冷色方案,…(4分)
∴两个气球同为冷色的概率为
| 6 |
| 20 |
| 3 |
| 10 |
(2)老师发出开始指令起计时,设牛牛完成任务的时刻为x,
老师来到牛牛身边检查情况的时刻为y,
则由题有
|
若当老师来到牛牛身边时牛牛已经完成任务,
则
|
如图所示,所求概率为几何概率
 (10分)
(10分)阴影部分(式2)面积为
| 1 |
| 2 |
可行域(式1)面积为(10-1)•(10-2)=72
∴当老师来到牛牛身边时牛牛已经完成任务的概率为
| 32 |
| 72 |
| 4 |
| 9 |
点评:本题考查概率的求法,是中档题,解题时要认真审题,注意可行域的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列函数中,最小正周期为π的是( )
A、y=tan
| ||
| B、y=|cosx| | ||
C、y=3sin(x-
| ||
| D、y=sin4x+π |