题目内容
已知f(x)=ax2-3x+6,不等式f(x)>4的解集为{x|x<1或x>b}.
(Ⅰ)求出a,b;
(Ⅱ)解不等式
>x.
(Ⅰ)求出a,b;
(Ⅱ)解不等式
| f(x) |
| x |
考点:一元二次不等式的解法
专题:不等式的解法及应用
分析:(Ⅰ)由题意,1、b是方程ax2-3x+6=4的两个根,结合根与系数的关系,求出a,b;
(Ⅱ)把不等式
>x化为
>x,整理求解,即得不等式的解集.
(Ⅱ)把不等式
| f(x) |
| x |
| x2-3x+6 |
| x |
解答:
解:(Ⅰ)根据题意,∵f(x)>4,
∴ax2-3x+6>4,
即ax2-3x+2>0;
又1、b是方程ax2-3x+2=0的两个根,
∴
,
解得
;
(Ⅱ)∵
>x,
∴
>x,
即
>0;
解得0<x<2,
∴不等式的解集是{x|0<x<2}.
∴ax2-3x+6>4,
即ax2-3x+2>0;
又1、b是方程ax2-3x+2=0的两个根,
∴
|
解得
|
(Ⅱ)∵
| f(x) |
| x |
∴
| x2-3x+6 |
| x |
即
| -3x+6 |
| x |
解得0<x<2,
∴不等式的解集是{x|0<x<2}.
点评:本题考查了不等式的解法与应用问题,解题时应根据一元二次不等式与对应的一元二次方程,结合根与系数的关系进行解答,是基础题.

练习册系列答案
相关题目
如图,D是直角△ABC斜边BC上一点,若AB=AD,AC=
DC,则sin∠ABD=( )
| 3 |

A、
| ||||
B、
| ||||
C、
| ||||
D、
|
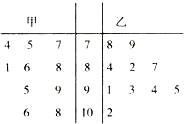 某次考试中,从甲、乙两个班各随机抽取10名学生的成绩进行统计分析,学生成绩的茎叶图如图所示,成绩不小于90分为及格.
某次考试中,从甲、乙两个班各随机抽取10名学生的成绩进行统计分析,学生成绩的茎叶图如图所示,成绩不小于90分为及格.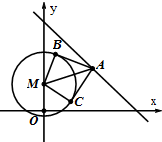 已知圆M:x2+y2-2y=24,直线l:x+y=11,l上一点A的横坐标为a,过点A作圆M的两条切线l1,l2,切点分别为B,C.
已知圆M:x2+y2-2y=24,直线l:x+y=11,l上一点A的横坐标为a,过点A作圆M的两条切线l1,l2,切点分别为B,C. 某幼儿园小班的美术课上,老师带领小朋友们用水彩笔为美术本上如右图所示的两个大小不同的气球涂色,要求一个气球只涂一种颜色,两个气球分别涂不同的颜色.该班的小朋友牛牛现可用的有暖色系水彩笔红色、橙色各一支,冷色系水彩笔绿色,蓝色,紫色各一支.
某幼儿园小班的美术课上,老师带领小朋友们用水彩笔为美术本上如右图所示的两个大小不同的气球涂色,要求一个气球只涂一种颜色,两个气球分别涂不同的颜色.该班的小朋友牛牛现可用的有暖色系水彩笔红色、橙色各一支,冷色系水彩笔绿色,蓝色,紫色各一支.