题目内容
19.已知△ABC在平面α内,直线CD⊥平面α,P是平面α内的一个动点,设P到直线AB的距离为d1,P到直线CD的距离为d2,若d1=d2,则动点P的轨迹是( )| A. | 圆 | B. | 抛物线 | C. | 椭圆 | D. | 双曲线 |
分析 由题意,在平面α内,P到直线AB的距离等于P到点C的距离,即可得出动点P的轨迹.
解答 解:由题意,在平面α内,P到直线AB的距离等于P到点C的距离,
∴动点P的轨迹是抛物线.
故选:B.
点评 本题考查轨迹方程,考查抛物线的定义,正确转化是关键.

练习册系列答案
相关题目
10.若x1,x2,x3,…,xn的平均数为$\overline x$,则x1+a,x2+a,…,xn+a的平均数为( )
| A. | $\overline x+a$ | B. | $a\overline x$ | C. | ${a^2}\overline x$ | D. | $\overline x+{a^2}$ |
7.若以F1(-3,0),F2(3,0)为焦点的双曲线与直线y=x-1有公共点,则该双曲线的离心率的最小值为( )
| A. | $\frac{\sqrt{6}}{2}$ | B. | $\frac{3\sqrt{5}}{5}$ | C. | $\frac{3}{2}$ | D. | $\sqrt{3}$ |
14.已知,M={x|x(x-1)<0},N={x|x>0},则M∩N等于( )
| A. | (0,1) | B. | (0,+∞) | C. | (0,1)∪(1,+∞) | D. | (-∞,1)∪(1,+∞) |
8.已知α,β∈($\frac{7π}{4}$,$\frac{9π}{4}$),则“tan2α>tan2β”是“3α>3β”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
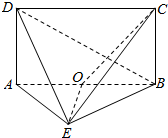 如图,多面体ABCDE中,ABCD是矩形,AB=2$\sqrt{2}$,BC=2,直线DA⊥平面ABE,AE=BE,O为棱AB的中点.
如图,多面体ABCDE中,ABCD是矩形,AB=2$\sqrt{2}$,BC=2,直线DA⊥平面ABE,AE=BE,O为棱AB的中点. 如图,在圆O:x2+y2=4上取一点A(-$\sqrt{3}$,1),E、F为y轴上的两点,且AE=AF,延长AE,AF分别与圆交于点MN.则直线MN的斜率为-$\sqrt{3}$.
如图,在圆O:x2+y2=4上取一点A(-$\sqrt{3}$,1),E、F为y轴上的两点,且AE=AF,延长AE,AF分别与圆交于点MN.则直线MN的斜率为-$\sqrt{3}$.