题目内容
某学校高一、高二、高三的三个年级学生人数如下表:
按年级分层抽样的方法评选优秀学生50人,其中高三有10人.
(Ⅰ)求z的值;
(Ⅱ)用分层抽样的方法在高一学生中抽取一个容量为5的样本.将该样本看成一个总体,从中任取2人,求至少有1名女生的概率.
| 高三 | 高二 | 高一 | |
| 女生 | 100 | 150 | z |
| 男生 | 300 | 450 | 600 |
(Ⅰ)求z的值;
(Ⅱ)用分层抽样的方法在高一学生中抽取一个容量为5的样本.将该样本看成一个总体,从中任取2人,求至少有1名女生的概率.
考点:列举法计算基本事件数及事件发生的概率,分层抽样方法
专题:概率与统计
分析:(Ⅰ)根据分层抽样的定义,建立方程关系,即可求z的值;
(Ⅱ)根据古典概型的概率公司,即可得到结论.
(Ⅱ)根据古典概型的概率公司,即可得到结论.
解答:
解:(Ⅰ)设该校总人数为n,
则由
=
,解得n=2000,
故z=2000-(100+300+150+450+600)=400;
(Ⅱ)设抽取样本中有m个女生,
则由分层抽样可知
=
,解得m=2.
即抽取2名女生,3名男生,分别记作a,b,A,B,C,
从中任取2个的基本事件为(a,b),(a,A),(a,B),(a,C),(b,A),(b,B),(b,C),(A,B),(A,C),(B,C),共10个.
至少含有1名女生的基本事件有7个,(a,b),(a,A),(a,B),(a,C),(b,A),(b,B),(b,C),
∴从中任取2人,求至少有1名女生的概率P=
.
则由
| 50 |
| n |
| 10 |
| 100+300 |
故z=2000-(100+300+150+450+600)=400;
(Ⅱ)设抽取样本中有m个女生,
则由分层抽样可知
| 400 |
| 1000 |
| m |
| 5 |
即抽取2名女生,3名男生,分别记作a,b,A,B,C,
从中任取2个的基本事件为(a,b),(a,A),(a,B),(a,C),(b,A),(b,B),(b,C),(A,B),(A,C),(B,C),共10个.
至少含有1名女生的基本事件有7个,(a,b),(a,A),(a,B),(a,C),(b,A),(b,B),(b,C),
∴从中任取2人,求至少有1名女生的概率P=
| 7 |
| 10 |
点评:本题主要考查分层抽样的应用,以及古典概率的计算,利用列举法是解决本题的关键.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
f(x)是R上的奇函数,当x≥0时,f(x)=x3+ln(1+x),则当x<0时,f(x)=( )
| A、-x3-ln(1-x) |
| B、-x3+ln(1-x) |
| C、x3-ln(1-x) |
| D、-x3+ln(1-x) |
函数y=xcosx是( )
| A、奇函数 | B、偶函数 |
| C、既奇又偶 | D、非奇非偶 |
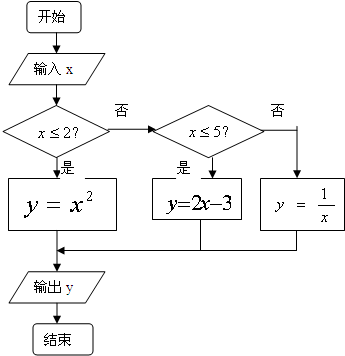 如图:
如图: