题目内容
20.若复数(1-ai)2(i为虚数单位,a∈R)是纯虚数,则a=( )| A. | 1 | B. | -1 | C. | 0 | D. | ±1 |
分析 利用复数代数形式的乘法运算化简,再由实部为0且虚部不为0求得a值.
解答 解:∵(1-ai)2=(1-a2)-2ai为纯虚数,
∴$\left\{\begin{array}{l}{1-{a}^{2}=0}\\{-2a≠0}\end{array}\right.$,解得a=±1.
故选:D.
点评 本题考查复数代数形式的乘除运算,考查了复数的基本概念,是基础的计算题.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
11.已知向量$\overrightarrow{a}$=(3,2),$\overrightarrow{b}$=(-1,1),则|2$\overrightarrow{a}+\overrightarrow{b}$|=( )
| A. | $\sqrt{2}$ | B. | $\sqrt{13}$ | C. | 5$\sqrt{2}$ | D. | $\sqrt{2}+2\sqrt{13}$ |
10.y=cos($\frac{π}{3}$+x)沿x轴向左平移φ(φ>0)个单位后的图象关于y轴对称,则φ的最小值是( )
| A. | $\frac{5}{6}π$ | B. | $\frac{2}{3}π$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{6}$ |
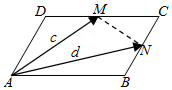 (1)如图,平行四边形ABCD中,M、N分别为DC、BC的中点,已知$\overrightarrow{AM}=\overrightarrow{c}$、$\overrightarrow{AN}=\overrightarrow{d}$,试用$\overrightarrow{c}$、$\overrightarrow{d}$表示$\overrightarrow{AB}$和$\overrightarrow{AD}$.
(1)如图,平行四边形ABCD中,M、N分别为DC、BC的中点,已知$\overrightarrow{AM}=\overrightarrow{c}$、$\overrightarrow{AN}=\overrightarrow{d}$,试用$\overrightarrow{c}$、$\overrightarrow{d}$表示$\overrightarrow{AB}$和$\overrightarrow{AD}$.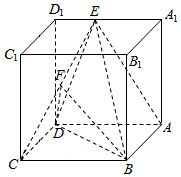 如图,正方体ABCD-A1B1C1D1中,点E是A1D1的中点,点F是CE的中点.
如图,正方体ABCD-A1B1C1D1中,点E是A1D1的中点,点F是CE的中点.