题目内容
5.若函数f(x)=log2(x2+ax+b)的定义域为(-∞,1)∪(3,+∞),则a=-4,b=3.分析 根据对数函数的定义,结合一元二次不等式的解集与对应方程的解之间的关系,利用根与系数的关系,即可求出a、b的值.
解答 解:∵函数f(x)=log2(x2+ax+b)的定义域为(-∞,1)∪(3,+∞),
∴不等式x2+ax+b>0解集是(-∞,1)∪(3,+∞),
∴方程x2+ax+b=0的两个实数根为1和3,
由根与系数的关系,得a=-(1+3)=-4,b=1×3=3;
故答案为:-4,3.
点评 本题考查了对数函数的定义与一元二次不等式解集的应用问题,也考查了根与系数关系的应用问题,是基础题目.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
13. 如图,矩形ABCD中,AB=3,BC=4,点M、N分别为边BC,CD上的动点,且MN=2,则$\overrightarrow{AM}$•$\overrightarrow{AN}$的最小值是( )
如图,矩形ABCD中,AB=3,BC=4,点M、N分别为边BC,CD上的动点,且MN=2,则$\overrightarrow{AM}$•$\overrightarrow{AN}$的最小值是( )
 如图,矩形ABCD中,AB=3,BC=4,点M、N分别为边BC,CD上的动点,且MN=2,则$\overrightarrow{AM}$•$\overrightarrow{AN}$的最小值是( )
如图,矩形ABCD中,AB=3,BC=4,点M、N分别为边BC,CD上的动点,且MN=2,则$\overrightarrow{AM}$•$\overrightarrow{AN}$的最小值是( )| A. | 13 | B. | 15 | C. | 17 | D. | 19 |
20.已知z=($\frac{1-i}{\sqrt{2}}$)2016(i是虚数单位),则z等于( )
| A. | -1 | B. | 1 | C. | 0 | D. | i |
10.y=cos($\frac{π}{3}$+x)沿x轴向左平移φ(φ>0)个单位后的图象关于y轴对称,则φ的最小值是( )
| A. | $\frac{5}{6}π$ | B. | $\frac{2}{3}π$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{6}$ |
11.设i为虚数单位,则$\frac{i}{2+i}$对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
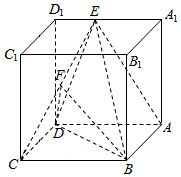 如图,正方体ABCD-A1B1C1D1中,点E是A1D1的中点,点F是CE的中点.
如图,正方体ABCD-A1B1C1D1中,点E是A1D1的中点,点F是CE的中点.