题目内容
已知数列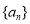 满足
满足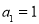 ,
,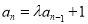 ,
,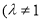 ,
,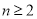 且
且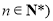 .
.
(1)求证:当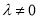 时,数列
时,数列 为等比数列;
为等比数列;
(2)如果 ,求数列
,求数列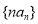 的前
的前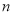 项和
项和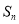 ;
;
(3)如果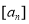 表示不超过
表示不超过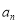 的最大整数,当
的最大整数,当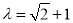 时,求数列
时,求数列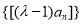 的通项公式.
的通项公式.
(1)证明见解析;(2) ;(3)
;(3) .
.
【解析】
试题分析:(1)根据题意构造新数列,利用 证明新数列的后一项与前一项之比为常数即可;(2)利用分组求和法与错位相减法进行求和;(3)找出
证明新数列的后一项与前一项之比为常数即可;(2)利用分组求和法与错位相减法进行求和;(3)找出 的通项,利用二项式定理进行求解.
的通项,利用二项式定理进行求解.
试题解析:(1)当 时,设
时,设 ,
,
则 当 时,
时, .
.
因为  ,
,
所以 
 为常数.
为常数.
因为  ,
,
所以 数列 是首项为
是首项为 ,公比为
,公比为 的等比数列. 4分
的等比数列. 4分
(2)由(1)知  时
时 为首项为
为首项为 ,公比为
,公比为 的是等比数列,
的是等比数列,
所以 .
.  .
.
设 ,
,
则 .
.
相减得
 .
.
设 ,
,


 .
.
即
 . 9分
. 9分
(3)由(1)可知 .
.
设 ,
,
由二项式定理可知 为整数,
为整数,
所以
 .
.
所以 .
.
考点:1.数列的递推公式;2.等差数列;3.错位相减法;4.二项式定理.

练习册系列答案
相关题目
 ,
,  ,则
,则 .
. 的焦点与双曲线
的焦点与双曲线 的焦点重合,则
的焦点重合,则 的值为 .
的值为 .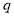 为公比的等比数列
为公比的等比数列 中,
中,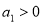 ,则“
,则“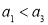 ”是“
”是“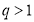 ”的( )
”的( )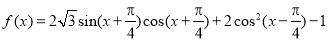 ,
,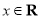 .
.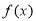 的最小正周期;
的最小正周期; 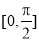 上的最大值和最小值及相应的x的值.
上的最大值和最小值及相应的x的值.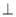 平面BCD,BC
平面BCD,BC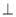 CD,若AB=BC=CD=2,则该三棱锥的侧视图(投影线平行于BD)的面积为( )
CD,若AB=BC=CD=2,则该三棱锥的侧视图(投影线平行于BD)的面积为( )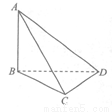
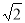 B.2 C.
B.2 C.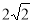 D.
D.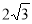
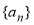 中,
中,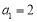 ,
,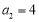 ,且
,且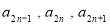 成等差数列,
成等差数列,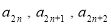 成等比数列,
成等比数列,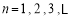 .
.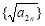 为等差数列;
为等差数列;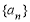 的通项公式.
的通项公式.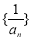 的前
的前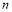 项和为
项和为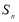 ,证明:
,证明: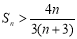 ,
,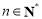 .
.