题目内容
10．设a，b是两个实数，以下能推出：“a，b中至少有一个大于1”的条件是（ ）| A． | a+b＞1 | B． | a+b=2 | C． | a2+b2＞2 | D． | a+b＞2 |
分析 A．若a=$\frac{1}{2}$，b=$\frac{2}{3}$，则a+b＞1，即可判断出结论；
B．若a=b=1，则a+b=2，即可判断出结论；
C．若a=-2，b=-3，则a2+b2＞2，即可判断出结论；
D．a+b＞2，满足：“a，b中至少有一个大于1”的条件，利用反证法即可证明．
解答 解：A．若a=$\frac{1}{2}$，b=$\frac{2}{3}$，则a+b＞1，因此A推不出；
B．若a=b=1，则a+b=2，故B推不出；
C．若a=-2，b=-3，则a2+b2＞2，故C推不出；
D．a+b＞2，满足：“a，b中至少有一个大于1”的条件，利用反证法：若a≤1，b≤1，则a+b≤2与已知a+b＞2矛盾，因此假设不正确．故原结论正确．
故选：D．
点评 本题考查了不等式的基本性质、反证法，考查了推理能力与计算能力，属于基础题．
练习册系列答案
相关题目
20．设a、b、l表示三条不同的直线，α、β、γ表示三个不同的平面，（ ）
| A． | 若α∩β=a，β∩γ=b，a∥b，则α∥γ | B． | 若a∥α，a∥β，b∥α，b∥β，则α∥β | ||
| C． | 若α⊥β，α∩β=a，b?β，a⊥b，则b⊥α | D． | 若a?α，b?α，l⊥α，l⊥b，则l⊥α |
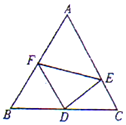如图，在边长为2的正三角形△ABC中，D为BC的中点，E，F分别在边CA，AB上．
如图，正三棱柱ABC-A1B1C1中，D，E，M分别是线段BC，CC1，AB的中点，AA1=2AB=4．
当前襄阳市正在积极创建文明城市，市某交警支队为调查市民文明驾车的情况，在市区某路口随机检测了40辆车的车速．现将所得数据分成六段：[60，65），[65，70），[70，75），[75，80），[80，85），[85，90），并绘得如图所示的频率分布直方图．