题目内容
2.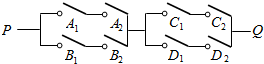 如图,在电路系统PQ中,用A1、A2、B1、B2、C1、C2、D1、D2表示8个开关,则使两端P、Q通电、不通电的开关闭合情况分别有(A)种、(D)种.
如图,在电路系统PQ中,用A1、A2、B1、B2、C1、C2、D1、D2表示8个开关,则使两端P、Q通电、不通电的开关闭合情况分别有(A)种、(D)种.| A.49 | B.56 | C.200 | D.207 | E.360 | F.269. |
分析 (1)根据分类计数原理即可求出;
(2)利用间接法,先求出所有的种数,再排除P、Q通电的种数.
解答 解:A1、A2为A种开关,B1、B2、为B种开关,C1、C2为C种开关D1、D2为D种开关,
(1)若通电,第一类A,B通一个,C,D通一个,C21C21=4种,剩下的4个开关,可以有C40+C41+C21C21=9种,共有4×9=36种,
第二类,A,B,C,D有3个通,C43=4种,剩下的2个开关,可以有C20+C21=3种,共有4×3=12种
第三类,A,B,C,D都通,有1种,
故有36+12+1=49种,
(2)A1、A2、B1、B2、C1、C2、D1、D2表示8个开关,可以开0个,1个,2个,3个,4个,5个,6个,7个,8个,故有C80+C81+C82+…+C88=28=256,
故不通的有256-49=207种,
故答案为:A,D.
点评 本题考查了排列组合问题,关键是分类,属于中档题.

练习册系列答案
相关题目
12.已知关于x的方程x2+ax+2b=0(a∈R,b∈R)的一个根在区间(0,1)内,另一个根在区间(1,2)内,则$\frac{a-1}{b-3}$的取值范围为($\frac{2}{3}$,2).
10.在平面直角坐标系xOy中,设A、B、C是圆x2+y2=1上相异三点.若存在正实数λ,μ,使得$\overrightarrow{OC}$=λ$\overrightarrow{OA}$+μ$\overrightarrow{OB}$,则(λ-2)2+μ2的取值范围是( )
| A. | ($\frac{1}{2}$,+∞) | B. | (-∞,2) | C. | (2,+∞) | D. | (-∞,$\frac{1}{2}$) |
7.sin750°的值是( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
11.函数f(x)=ex+2x-3的零点所在区间是( )
| A. | (-2,-1) | B. | (-1,0) | C. | (1,2) | D. | (0,1) |
12.sin80°sin40°-cos80°cos40°的值为( )
| A. | -$\frac{\sqrt{3}}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |