题目内容
椭圆
+
=1(a>0)的焦点在x轴上,则它的离心率的最大值为 .
| x2 |
| 4a |
| y2 |
| a2+1 |
考点:椭圆的简单性质
专题:综合题,圆锥曲线的定义、性质与方程
分析:先确定a的范围,求出椭圆的离心率,利用基本不等式,即可得出结论.
解答:
解:∵椭圆
+
=1(a>0)的焦点在x轴上,
∴4a>a2+1,
∴2-
<a<2+
.
椭圆的离心率e满足:e2=
=1-
(a+
),
∵2-
<a<2+
.
∴a+
≥2,
∴e2≤1-
=
,当且仅当a=
,即a=1时,e2有最大值
.
由此可得椭圆的离心率e的最大值为
.
故答案为:
.
| x2 |
| 4a |
| y2 |
| a2+1 |
∴4a>a2+1,
∴2-
| 3 |
| 3 |
椭圆的离心率e满足:e2=
| 4a-a2-1 |
| 4a |
| 1 |
| 4 |
| 1 |
| a |
∵2-
| 3 |
| 3 |
∴a+
| 1 |
| a |
∴e2≤1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| a |
| 1 |
| 2 |
由此可得椭圆的离心率e的最大值为
| ||
| 2 |
故答案为:
| ||
| 2 |
点评:本题考查椭圆的离心率,考查基本不等式,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
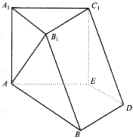 如图,在六面体A1B1C1D1中,平面A1B1C1∥平面ABDE,△A1B1C1是正三角形,四边形AA1B1B是直角梯形,AB⊥AA1,四边形AEC1A1为正方形,四边形ABDE是等腰梯形,AB∥DE,AB=2AE=2DE=2.
如图,在六面体A1B1C1D1中,平面A1B1C1∥平面ABDE,△A1B1C1是正三角形,四边形AA1B1B是直角梯形,AB⊥AA1,四边形AEC1A1为正方形,四边形ABDE是等腰梯形,AB∥DE,AB=2AE=2DE=2.