题目内容
设命题p:实数x满足x2-4ax+3a2<0,其中a>0;命题q:实数x满足2<x≤3.
(Ⅰ)若a=1,且p∧q为真,求实数x的取值范围;
(Ⅱ)若¬p是¬q的充分不必要条件,求实数a的取值范围.
(Ⅰ)若a=1,且p∧q为真,求实数x的取值范围;
(Ⅱ)若¬p是¬q的充分不必要条件,求实数a的取值范围.
考点:必要条件、充分条件与充要条件的判断,复合命题的真假
专题:简易逻辑
分析:(I)利用一元二次不等式的解法可化简命题p,若p∧q为真,则p真且q真,即可得出;
(II)¬p是¬q的充分不必要条件,即¬p⇒¬q,且¬q?¬p,即可得出.
(II)¬p是¬q的充分不必要条件,即¬p⇒¬q,且¬q?¬p,即可得出.
解答:
解:(Ⅰ)对于命题p:由x2-4ax+3a2<0得(x-3a)(x-a)<0,
又a>0,∴a<x<3a,
当a=1时,1<x<3,即p为真时实数x的取值范围是1<x<3.
由已知q为真时实数x的取值范围是2<x≤3.
若p∧q为真,则p真且q真,
∴实数x的取值范围是2<x<3.
(Ⅱ)¬p是¬q的充分不必要条件,即¬p⇒¬q,且¬q?¬p,
设A={x|¬p},B={x|¬q},则A?B,
又A={x|¬p}={x|x≤a或x≥3a},B={x|¬q}={x≤2或x>3},
则0<a≤2且3a>3,
∴实数a的取值范围是1<a≤2.
又a>0,∴a<x<3a,
当a=1时,1<x<3,即p为真时实数x的取值范围是1<x<3.
由已知q为真时实数x的取值范围是2<x≤3.
若p∧q为真,则p真且q真,
∴实数x的取值范围是2<x<3.
(Ⅱ)¬p是¬q的充分不必要条件,即¬p⇒¬q,且¬q?¬p,
设A={x|¬p},B={x|¬q},则A?B,
又A={x|¬p}={x|x≤a或x≥3a},B={x|¬q}={x≤2或x>3},
则0<a≤2且3a>3,
∴实数a的取值范围是1<a≤2.
点评:本题考查了简易逻辑的有关知识、一元二次不等式的解法,考查了推理能力和计算能力,属于基础题.

练习册系列答案
相关题目
(
-
)n的展开式中只有第5项的二项式系数最大,则展开式中的常数项是( )
| 3 | x |
| 1 |
| x |
| A、28 | B、-28 |
| C、70 | D、-70 |
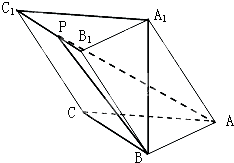 在三棱柱ABC-A1B1C1中,已知AB=BC=2,∠ABC=90°,点A1在底面ABC的投影为B,且A1B=2
在三棱柱ABC-A1B1C1中,已知AB=BC=2,∠ABC=90°,点A1在底面ABC的投影为B,且A1B=2