Question

已知椭圆

x2

a2

+

y2

b2

=1(a＞b＞0)的半焦距为C，（C＞0），左焦点为F，右顶点为A，抛物线y²=

15

8

（a+c）x与椭圆交于B，C两点，若四边形ABFC是菱形，则椭圆的离心率是

 

．

Answer 1

考点：椭圆的简单性质

专题：计算题,圆锥曲线的定义、性质与方程

分析：根据四边形ABFC是菱形得到B的横坐标为

1

2

（a-c），代入抛物线方程求出B的纵坐标为

15

4

b，因此将点B的坐标代入椭圆方程，化简整理得到关于椭圆离心率e的方程，即可得到该椭圆的离心率．

解答： 解：∵椭圆

x2

a2

+

y2

b2

=1(a＞b＞0)的左焦点为F，右顶点为A，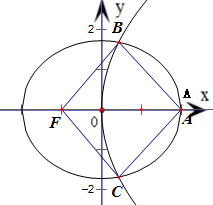
∴A（a，0），F（-c，0）
∵抛物线y²=

15

8

（a+c）x与椭圆交于B，C两点，
∴B、C两点关于x轴对称，可设B（m，n），C（m，-n）
∵四边形ABFC是菱形，∴m=

1

2

（a-c）
将B（m，n）代入抛物线方程，得
n²=

15

8

（a+c）（a-c）=

15

16

b²
∴B（

1

2

（a-c），

15

4

b），再代入椭圆方程，得

[ 1 2 (a-c)]2

a2

+

( 15 4 b)2

b2

=1
化简整理，得4e²-8e+3=0，解之得e=

1

2

（e=

3

2

＞1不符合题意，舍去）
故答案为：

1

2

．

点评：本题给出椭圆与抛物线相交得到菱形ABFC，求椭圆的离心率e，着重考查了椭圆、抛物线的标准方程和简单几何性质等知识，属于中档题．