题目内容
13.在△ABC中,角A,B,C所对的边分别为a,b,c.(Ⅰ)若b2+c2=a2+bc,求角A的大小;
(Ⅱ)若acosA=bcosB,试判断△ABC的形状.
分析 (Ⅰ)由已知利用余弦定理可得cosA=$\frac{1}{2}$,又结合∠A是△ABC的内角,即可求A的值.
(Ⅱ)由正弦定理得sinAcosA=sinBcosB,可得sin2A=sin2B.利用正弦函数的图象和性质可得2A=2B或2A+2B=π,即可得解.
解答 解:(Ⅰ)∵由已知得cosA=$\frac{b2+c2-a2}{2bc}$=$\frac{bc}{2bc}$=$\frac{1}{2}$,…(3分)
又∵∠A是△ABC的内角,
∴A=$\frac{π}{3}$.…(5分)
(Ⅱ)在△ABC中,由acosA=bcosB,得sinAcosA=sinBcosB,…(6分)
∴sin2A=sin2B.…(7分)
∴2A=2B或2A+2B=π.…(9分)
∴A=B或$A+B=\frac{π}{2}$
∴△ABC是等腰三角形或直角三角形.…(10分)
点评 本题主要考查了正弦定理,余弦定理,正弦函数的图象和性质,考查了转化思想和数形结合思想的应用,属于中档题.

练习册系列答案
相关题目
1.矩形ABCD中,AB=2$\sqrt{3}$,AD=2,点E、F分别为线段BC、CD边上的动点,且满足EF=1,则$\overrightarrow{AE}$$•\overrightarrow{AF}$的最小值是( )
| A. | 12 | B. | 16 | C. | 20 | D. | 24 |
8.在△ABC中,$c=1,\;A=\frac{π}{4},\;\;C=\frac{π}{3}$,则a等于( )
| A. | $\frac{{\sqrt{2}}}{3}$ | B. | $\frac{{\sqrt{3}}}{3}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{{\sqrt{6}}}{3}$ |
18.函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则( )
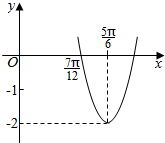

| A. | 函数f(x)在区间[0,$\frac{π}{2}$]上单调递增 | B. | 函数f(x)在区间[0,$\frac{π}{2}$]上单调递减 | ||
| C. | 函数f(x)在区间[0,$\frac{π}{2}$]上的最小值为-2 | D. | 函数f(x)在区间[0,$\frac{π}{2}$]上的最小值为-1 |
5.已知向量$\overrightarrow{m}$=(sinA,$\frac{1}{2}$)与向量$\overrightarrow{n}$=(3,sinA+$\sqrt{3}$cosA)共线,其中A是△ABC的内角,则角A的大小为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
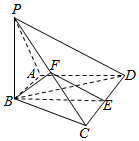 如图,在四棱锥P-ABCD中,AB⊥PA,AB∥CD,且PB=BC=BD=$\sqrt{6}$,CD=2AB=2$\sqrt{2}$,∠PAD=120°,E和F分别是棱CD和PC的中点.
如图,在四棱锥P-ABCD中,AB⊥PA,AB∥CD,且PB=BC=BD=$\sqrt{6}$,CD=2AB=2$\sqrt{2}$,∠PAD=120°,E和F分别是棱CD和PC的中点.