题目内容
已知命题p:方程
-
=1表示焦点在y轴上的椭圆;命题q:双曲线
-
=1的离心率e∈(1,2).
若命题p、q满足:p∧q为假,p∨q为真,求m的取值范围.
| x2 |
| 2m |
| y2 |
| m-1 |
| y2 |
| 5 |
| x2 |
| m |
若命题p、q满足:p∧q为假,p∨q为真,求m的取值范围.
考点:双曲线的简单性质,复合命题的真假
专题:圆锥曲线的定义、性质与方程
分析:先化简两个命题中的条件,再根据复合命题真假的判断得出p假q真,即可得出参数的取值范围
解答:
解:由P得:
⇒0<m<
,…(4分)
由命题Q得:
⇒0<m<15,…(8分)
由已知命题p、q满足:p∧q为假,p∨q为真,结合两个条件可得,p假q真
故m的取值范围是
≤m<15 …(12分)
|
| 1 |
| 3 |
由命题Q得:
|
由已知命题p、q满足:p∧q为假,p∨q为真,结合两个条件可得,p假q真
故m的取值范围是
| 1 |
| 3 |
点评:本题非条件考查椭圆与双曲线的性质,复合命题的真假判断,涉及到的知识点较多,综合性较强,熟练掌握相关的知识是解答的关键

练习册系列答案
相关题目
已知复数Z=
(i为虚数单位)在复平面内对应的点在直线x-2y+m=0上,则m=( )
| 4+2i |
| (1+i)2 |
| A、-5 | B、-3 | C、3 | D、5 |
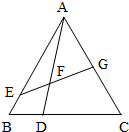 如图,在△ABC中,已知CD=2DB,BA=5BE,AF=mAD,AG=tAC,设
如图,在△ABC中,已知CD=2DB,BA=5BE,AF=mAD,AG=tAC,设