Question

如图所示的多面体中，DB⊥平面ABC，AE∥DB，且△ABE是边长为2的等边三角形，AE=1，BD=2．
（1）在线段DC上是否存在一点F，使得EF⊥平面DBC，若存在，求线段DF的长度，若不存在，说明理由；
（2）求二面角D-EC-B的平面角的余弦值．

Answer 1

考点：二面角的平面角及求法,直线与平面垂直的性质

专题：圆锥曲线中的最值与范围问题

分析：（1）取CD的中点为F，BC的中点为H，由已知条件得AEFH为平行四边形，从而EF∥AH，进而AH⊥平面BCD，EF⊥平面DBC，由此推导出存在F为CD中点，DF=

2

时，使得EF⊥面DBC．
（2）建立空间直角坐标系，利用向量法能求出二面角D-EC-B的余弦值．

解答： 解：（1）取CD的中点为F，BC的中点为H，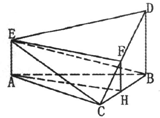
∵FH

∥

.

1

2

BD，AE

∥

.

1

2

BD，
∴AEFH为平行四边形，∴EF∥AH，
△ABC是等边三角形，DB⊥平面ABC，
∵AH⊥BC，AH⊥BD，BC∩BD=B，
∴AH⊥平面BCD，
∴EF⊥平面DBC，
BC=2，BD=2，∴DE=

1

2

CD=

2

，
存在F为CD中点，DF=

2

时，
使得EF⊥面DBC．
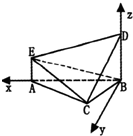
（2）如图建立空间直角坐标系，
由C（1，

3

，0），B（0，0，0），
E（2，0，1），D（0，0，2），

BE

=(2，0，1)，

EC

=(-1，

3

，-1)，

DE

=(2，0，-1)，
设

n

=(x，y，z)是平面BCE的法向量，
则

n • BE =2x+z=0 n • EC =-x+ 3 y-z=0

，
取x=1，得

n

=(1，-

3

3

，-2)，
设

m

=（a，b，c）为平面CDE的法向量，
则

m • DE =2a-c=0 m • EC =-a+ 3 b-c=0

，
取a=1，得

m

=(1，

3

，2)，
∴cos＜

n

，

m

＞=

-4

8 6 3

=-

6

4

，
∴二面角D-EC-B的余弦值为

6

4

．

点评：本题考查满足条件的点是否存在的判断与求法，考查二面角的余弦值的求法，解题时要认真审题，注意向量法的合理运用．