题目内容
14.在锐角△ABC的内角A,B,C的对边分别为a,b,c,且$\sqrt{3}$a=2csinA.(1)确定角C的大小;
(2)若c=$\sqrt{7}$,且ab=6,求边a,b.
分析 (1)由已知及正弦定理得$\frac{a}{c}$=$\frac{2sinA}{\sqrt{3}}$=$\frac{sinA}{sinC}$,结合sinA>0,可求sinC=$\frac{\sqrt{3}}{2}$,根据已知可求C=$\frac{π}{3}$.
(2)由余弦定理,ab=6,可求a2+b2=1,联立即可解得a,b的值.
解答 (本小题满分12分)
解:(1)由$\sqrt{3}$a=2csinA及正弦定理得$\frac{a}{c}$=$\frac{2sinA}{\sqrt{3}}$=$\frac{sinA}{sinC}$,-------(4分)(知道用正弦定理2分)
因为sinA>0,故sinC=$\frac{\sqrt{3}}{2}$,
又锐角△ABC,所以C=$\frac{π}{3}$.---------------------------------------------(6分)
(2)由余弦定理a2+b2-2abcos$\frac{π}{3}$=7,-----------------(9分)(余弦定理2分)
ab=6,得a2+b2=1,
解得:$\left\{\begin{array}{l}{a=2}\\{b=3}\end{array}\right.$或$\left\{\begin{array}{l}{a=3}\\{b=2}\end{array}\right.$.-----------------------------------(12分)
点评 本题主要考查了正弦定理,余弦定理在解三角形中的应用,考查了计算能力和转化思想,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.函数f(x)定义在(-∞,+∞)上.则“曲线:y=f(x)过原点”是“f(x)为奇函数”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
4.设函数f(x),g(x)在区间(0,5)内导数存在,且有以下数据:
则函数y=f(x)•g(x)在x=2处的导数值是16;曲线f(x)在点(1,f(1))处的切线方程是y=3x-1.
| x | 1 | 2 | 3 | 4 |
| f(x) | 2 | 3 | 4 | 1 |
| f′(x) | 3 | 4 | 2 | 1 |
| g(x) | 3 | 1 | 4 | 2 |
| g′(x) | 2 | 4 | 1 | 3 |
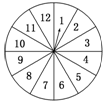 某种日用品上市以后供不应求,为满足更多的消费者,某商场在销售的过程中要求购买这种产品的顾客必须参加如下活动:摇动如下图所示的游戏转盘(上面扇形的圆心角都相等),按照指针所指区域的数字购买商品的件数,每人只能参加一次这个活动.
某种日用品上市以后供不应求,为满足更多的消费者,某商场在销售的过程中要求购买这种产品的顾客必须参加如下活动:摇动如下图所示的游戏转盘(上面扇形的圆心角都相等),按照指针所指区域的数字购买商品的件数,每人只能参加一次这个活动.