题目内容
15.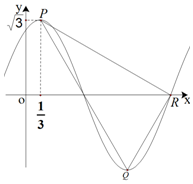 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0),其部分图象如图所示,点P,Q分别为图象上相邻的最高点与最低点,R是图象与x轴的交点,若P点的横坐标为$\frac{1}{3}$,f($\frac{1}{3}$)=$\sqrt{3}$,PR⊥QR,则函数f(x)的解析式可以是( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0),其部分图象如图所示,点P,Q分别为图象上相邻的最高点与最低点,R是图象与x轴的交点,若P点的横坐标为$\frac{1}{3}$,f($\frac{1}{3}$)=$\sqrt{3}$,PR⊥QR,则函数f(x)的解析式可以是( )| A. | $f(x)=\sqrt{3}sin(\frac{π}{2}x+\frac{π}{3})$ | B. | $f(x)=\sqrt{3}sin(\frac{π}{2}x-\frac{π}{6})$ | ||
| C. | $f(x)=\sqrt{3}sin(\frac{2π}{3}x+\frac{5π}{18})$ | D. | $f(x)=\sqrt{3}sin(πx+\frac{π}{6})$ |
分析 由已知可得A=$\sqrt{3}$,设其周期为T,则:P($\frac{1}{3}$,$\sqrt{3}$),R($\frac{1}{3}+$$\frac{3T}{4}$,0),Q($\frac{1}{3}$+$\frac{1}{2}$T,-$\sqrt{3}$),由两点间距离公式,勾股定理可求T,利用周期公式可求ω,由f($\frac{1}{3}$)=$\sqrt{3}$,可得φ,即可得解函数解析式.
解答 解:由已知可得A=$\sqrt{3}$,
设其周期为T,则:P($\frac{1}{3}$,$\sqrt{3}$),R($\frac{1}{3}+$$\frac{3T}{4}$,0),Q($\frac{1}{3}$+$\frac{1}{2}$T,-$\sqrt{3}$),
由于PR⊥QR,可得:PR2+RQ2=PQ2,
可得:($\frac{1}{3}+$$\frac{3T}{4}$-$\frac{1}{3}$)2+(0-$\sqrt{3}$)2+($\frac{1}{3}$+$\frac{1}{2}$T-$\frac{1}{3}$-$\frac{3T}{4}$)2+(-$\sqrt{3}$-0)2=($\frac{1}{3}+$$\frac{1}{2}T$-$\frac{1}{3}$)2+(-$\sqrt{3}$-$\sqrt{3}$)2,
整理可得:T2=16,解得:T=4,ω=$\frac{2π}{T}$=$\frac{π}{2}$,
由于f($\frac{1}{3}$)=$\sqrt{3}$,可得:$\sqrt{3}$sin($\frac{π}{2}$×$\frac{1}{3}$+φ)=$\sqrt{3}$,
所以,φ+$\frac{π}{6}$=2kπ+$\frac{π}{2}$,k∈Z,解得:φ=2kπ+$\frac{π}{3}$,k∈Z,
所以,当k=0时,φ=$\frac{π}{3}$,函数f(x)的解析式是f(x)=$\sqrt{3}$sin($\frac{π}{2}$x+$\frac{π}{3}$).
故选:A.
点评 本题主要考查了由y=Asin(ωx+φ)的部分图象确定其解析式,考查了勾股定理及正弦函数的图象和性质的应用,考查了数形结合思想,属于基础题.

 阅读快车系列答案
阅读快车系列答案| A. | {0,1} | B. | {0} | C. | {2,3} | D. | {1,2,3} |
| A. | -2 | B. | 2 | C. | -2i | D. | 2i |
| x | 1 | 2 | 3 | 4 |
| f(x) | 2 | 3 | 4 | 1 |
| f′(x) | 3 | 4 | 2 | 1 |
| g(x) | 3 | 1 | 4 | 2 |
| g′(x) | 2 | 4 | 1 | 3 |