题目内容
14.已知方程|ln|x-2||=m(x-2)2,有且仅有四个解x1,x2,x3,x4,则m(x1+x2+x3+x4)=$\frac{4}{e}$.分析 作出两侧函数的图象,根据对称性可知x1+x2+x3+x4=8,根据图象有4个交点可知两图象相切,利用导数的几何意义求出m即可计算答案.
解答 解:令f(x)=|ln|x-2||,g(x)=m(x-2)2,
则f(x)与g(x)的图象均关于直线x=2对称,
∴x1+x2+x3+x4=8,
作出f(x)与g(x)的函数图象如图所示: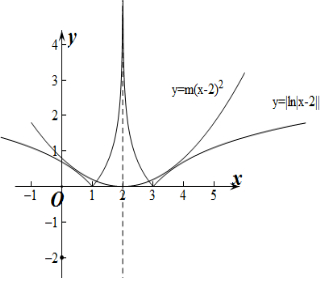
∵方程|ln|x-2||=m(x-2)2有且仅有四个解,
∴y=m(x-2)2与y=ln(x-2)相切,
设切点为(x0,y0),则$\left\{\begin{array}{l}{{y}_{0}=m({x}_{0}-2)^{2}}\\{{y}_{0}=ln({x}_{0}-2)}\\{2m({x}_{0}-2)=\frac{1}{{x}_{0}-2}}\end{array}\right.$,解得x0=$\sqrt{e}$+2,m=$\frac{1}{2e}$.
∴m(x1+x2+x3+x4)=$\frac{4}{e}$.
故答案为:$\frac{4}{e}$.
点评 本题考查了方程的根与函数图象的关系,导数的几何意义,属于中档题.

练习册系列答案
相关题目
2.设k1,k2分别是两条直线l1,l2的斜率,则“l1∥l2”是“k1=k2”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
19.已知$tan({α+\frac{π}{4}})=\frac{3}{4}$,则${cos^2}({\frac{π}{4}-α})$=( )
| A. | $\frac{7}{25}$ | B. | $\frac{9}{25}$ | C. | $\frac{16}{25}$ | D. | $\frac{24}{25}$ |