题目内容
6.已知函数$f(x)=(\frac{x^2}{2}-kx)lnx+\frac{x^2}{4}$.(Ⅰ)若f(x)在定义域内单调递增,求实数k的值;
(Ⅱ)若f(x)的极小值大于0,求实数k的取值范围.
分析 (Ⅰ)求出函数的导数,解关于导函数的方程,求出k的值即可;
(Ⅱ)通过讨论k的范围,判断f′(x)的符号,得到函数f(x)的单调区间,求出k的范围即可.
解答 解:(Ⅰ)依题意可知f'(x)=(x-k)(lnx+1),令f'(x)=0,可得x1=k,${x_2}=\frac{1}{e}$.
若x1≠x2,则在x1,x2之间存在一个区间,使得f'(x)<0,不满足题意.
因此x1=x2,即$k=\frac{1}{e}$.
(Ⅱ)当$k<\frac{1}{e}$时,若k>0,则f'(x)在$(k,\frac{1}{e})$上小于0,在$(\frac{1}{e},+∞)$上大于0,
若k≤0,则f'(x)在$(0,\frac{1}{e})$上小于0,在$(\frac{1}{e},+∞)$上大于0,
因此$x=\frac{1}{e}$是极小值点,$f(\frac{1}{e})=\frac{k}{e}-\frac{1}{{4{e^2}}}>0$,解得$k>\frac{1}{4e}$.
当$k>\frac{1}{e}$时,f'(x)在$(\frac{1}{e},k)$上小于0,在(k,+∞)上大于0,
因此x=k是极小值点,$f(k)=\frac{k^2}{4}(1-2lnk)>0$,解得$k<\sqrt{e}$.
当$k=\frac{1}{e}$时,f(x)没有极小值点,不符合题意.
综上可得$k∈(\frac{1}{4e},\frac{1}{e})∪(\frac{1}{e},\sqrt{e})$.
点评 本题考查了函数的单调性、极值问题,考查导数的应用以及分类讨论思想、转化思想,是一道中档题.

练习册系列答案
相关题目
16.在Rt△ABC中,CA=4,CB=3,M,N是斜边AB上的两个动点,且MN=2,则$\overrightarrow{CM}$•$\overrightarrow{CN}$的取值范围为( )
| A. | $[2,\frac{5}{2}]$ | B. | [4,6] | C. | $[\frac{119}{25},\frac{48}{5}]$ | D. | $[\frac{144}{25},\frac{53}{5}]$ |
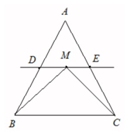 在△ABC中,D、E分别是AB,AC的中点,M是直线DE上的动点,若△ABC的面积为1,则$\overrightarrow{MB}$•$\overrightarrow{MC}$+$\overrightarrow{BC}$2的最小值为$\sqrt{3}$.
在△ABC中,D、E分别是AB,AC的中点,M是直线DE上的动点,若△ABC的面积为1,则$\overrightarrow{MB}$•$\overrightarrow{MC}$+$\overrightarrow{BC}$2的最小值为$\sqrt{3}$.