已知△ABC内角A.B.C的对边分别是a.b.c.若$cosB=\frac{1}{4}.b=3$.sinC=2sinA.则△ABC的面积为$\frac{9\sqrt{15}}{16}$．题目和参考答案——青夏教育精英家教网——

题目内容

4．已知△ABC内角A，B，C的对边分别是a，b，c，若$cosB=\frac{1}{4}，b=3$，sinC=2sinA，则△ABC的面积为$\frac{9\sqrt{15}}{16}$．

分析由题意和正余弦定理可得a，c的值，由同角三角函数的基本关系可得sinB，代入三角形的面积公式计算可得．

解答解：在△ABC中由正弦定理可知：$\frac{a}{sinA}$=$\frac{b}{sinB}$=$\frac{c}{sinC}$=2R，
由sinC=2sinA，则c=2a，
cosB=$\frac{1}{4}$，sinB=$\sqrt{1-co{s}^{2}B}$=$\frac{\sqrt{15}}{4}$，
由余弦定理可知：b²=a²+c²-2accosB，即3²=a²+（2a）²-2a•2a×$\frac{1}{4}$，
解得a=$\frac{3}{2}$，c=3，
△ABC的面积S=$\frac{1}{2}$acsinB=$\frac{1}{2}$×$\frac{3}{2}$×3×$\frac{\sqrt{15}}{4}$=$\frac{9\sqrt{15}}{16}$，
故答案为：$\frac{9\sqrt{15}}{16}$，．

点评本题考查三角形的面积，涉及正余弦定理的应用，属基础题．

练习册系列答案

课堂作业广西教育出版社系列答案

赢在起跑线天天100分小学优化测试卷系列答案

目标测试系列答案

单元评价卷宁波出版社系列答案

熠光传媒名师好卷系列答案

英才小灵通系列答案

顶尖训练系列答案

课堂360系列答案

黄冈课堂系列答案

全优设计课时作业本系列答案

相关题目

14．已知方程|ln|x-2||=m（x-2）²，有且仅有四个解x₁，x₂，x₃，x₄，则m（x₁+x₂+x₃+x₄）=$\frac{4}{e}$．

15．已知数列{a_n}的前n项和S_n满足a_n=1-2S_n．
（1）求证：数列{a_n}为等比数列；
（2）设函数$f（x）={log_{\frac{1}{3}}}x，{b_n}=f（{a_1}）+f（{a_2}）+…+f（{a_n}）$，求T_n=$\frac{1}{b_1}+\frac{1}{b_2}+\frac{1}{b_3}+…+\frac{1}{b_n}$．

12．点M，N分别是正方体ABCD-A₁B₁C₁D₁的棱BB₁和B₁C₁的中点，则MN和CD₁所成角的大小为（　　）

如图，在△ABC中，已知B=45°，D是BC边上的一点，AD=4，AC=2$\sqrt{7}$，DC=2
（1）求cos∠ADC
（2）求AB．

9．已知函数$f（x）=sin（2x+\frac{π}{6}）+sin（2x-\frac{π}{6}）+cos2x+1$
（1）求函数f（x）的最小正周期和函数的单调递增区间；
（2）已知△ABC中，角A，B，C的对边分别为a，b，c，若$f（A）=3，B=\frac{π}{4}，a=\sqrt{3}$，求AB．

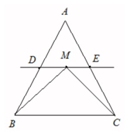在△ABC中，D、E分别是AB，AC的中点，M是直线DE上的动点，若△ABC的面积为1，则$\overrightarrow{MB}$•$\overrightarrow{MC}$+$\overrightarrow{BC}$²的最小值为$\sqrt{3}$．

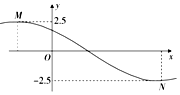已知函数f（x）=2.5cos（ωx+φ）（ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示，M、N两点之间的距离为13，且f（3）=0，若将函数f（x）的图象向右平移t（t＞0）个单位长度后所得函数的图象关于坐标原点对称，则t的最小值为（　　）

14．已知偶函数f（x）在区间（-∞，0]内单调递减，a=f（log₂3），b=f（log₄5），$c=f（{2^{\frac{1}{2}}}）$，则a，b，c满足（　　）