题目内容
19.已知$tan({α+\frac{π}{4}})=\frac{3}{4}$,则${cos^2}({\frac{π}{4}-α})$=( )| A. | $\frac{7}{25}$ | B. | $\frac{9}{25}$ | C. | $\frac{16}{25}$ | D. | $\frac{24}{25}$ |
分析 利用同角三角函数的基本关系、诱导公式,求得要求式子的值.
解答 解:∵$tan({α+\frac{π}{4}})=\frac{3}{4}$,
∴${cos^2}({\frac{π}{4}-α})$=${sin}^{2}(α+\frac{π}{4})$=$\frac{{sin}^{2}(α+\frac{π}{4})}{{sin}^{2}(α+\frac{π}{4}){+cos}^{2}(α+\frac{π}{4})}$=$\frac{1}{1+\frac{{cos}^{2}(α+\frac{π}{4})}{{sin}^{2}(α+\frac{π}{4})}}$=$\frac{1}{1+\frac{1}{{tan}^{2}(α+\frac{π}{4})}}$=$\frac{1}{1+\frac{16}{9}}$=$\frac{9}{25}$,
故选:B.
点评 本题主要考查同角三角函数的基本关系、诱导公式的应用,属于基础题.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
9.若一个正四面体的表面积为S1,其内切球的表面积为S2,则$\frac{S_1}{S_2}$=( )
| A. | $\frac{6}{π}$ | B. | $\frac{{6\sqrt{3}}}{π}$ | C. | $\frac{4}{3}$ | D. | $\frac{{4\sqrt{3}}}{π}$ |
8.设Q表示要证明的结论,P表示一个明显成立的条件,那么下列流程图表示的证明方法是( )
Q?P1→P1?P2→P2?P3→…→得到一个明显成立的条件.
Q?P1→P1?P2→P2?P3→…→得到一个明显成立的条件.
| A. | 综合法 | B. | 分析法 | C. | 反证法 | D. | 比较法 |
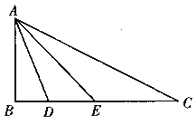 如图,在△ABC中,∠B=90°,∠BAD=∠DAE=∠EAC,BD=2,DE=3.
如图,在△ABC中,∠B=90°,∠BAD=∠DAE=∠EAC,BD=2,DE=3.