题目内容
 已知函数f(x)=sin[ωπ(x+
已知函数f(x)=sin[ωπ(x+| 1 |
| 3 |
| 1 |
| 2 |
(1)求函数f(x)的解析式;
(2)已知角α、β、θ满足f(
| 2 |
| π |
| 1 |
| 3 |
| 2 |
| π |
| 1 |
| 3 |
2
| ||
| 3 |
| 3π |
| 4 |
| sin(θ+α)sin(θ+β) |
| cos2θ |
考点:由y=Asin(ωx+φ)的部分图象确定其解析式,三角函数中的恒等变换应用
专题:三角函数的图像与性质
分析:(1)由tan∠APB=
列式求出周期,再由周期公式求出ω,则函数解析式可求;
(2)把
α-
,
β-
分别代入f(x),由f(
α-
)•f(
β-
)=
结合α+β=
得到矛盾的式子,说明
的值不存在.
| 1 |
| 2 |
(2)把
| 2 |
| π |
| 1 |
| 3 |
| 2 |
| π |
| 1 |
| 3 |
| 2 |
| π |
| 1 |
| 3 |
| 2 |
| π |
| 1 |
| 3 |
2
| ||
| 3 |
| 3π |
| 4 |
| sin(θ+α)sin(θ+β) |
| cos2θ |
解答:
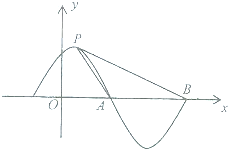
 解:(1)如图,
解:(1)如图,
过P作PM⊥x轴,垂足是M,
则tan∠MPB=
=
,tan∠MPA=
=
.
∴tan∠APB=tan(∠MPB-∠MPA)=
=
=
,
解得:T=4或T=
.
∵f(x)=sin[ωπ(x+
)]=sin(ωπx+
ωπ),
∴
=4或
=
,得ω=
或ω=
.
∴f(x)=sin(
πx+
π)或f(x)=sin(
πx+
π);
(2)当f(x)=sin(
πx+
π)时,
由f(
α-
)•f(
β-
)=
,得
sin[
π(
α-
)+
]•sin[
π(
β-
)+
π]=
.
即sinα•sinβ=
,则-
[cos(α+β)-cos(α-β)]=
,
由α+β=
,得:cos(α-β)=
>1,矛盾;
当f(x)=sin(
πx+
π)时,
由f(
α-
)•f(
β-
)=
,得
sin[
π(
α-
)+
]•sin[
π(
β-
)+
]=
.
即sin3α•sin3β=
.则-
[cos3(α+β)-cos3(α-β)]=
.
由α+β=
,得cos3(α-β)=
>1,矛盾.
∴
的值不存在.
 解:(1)如图,
解:(1)如图,过P作PM⊥x轴,垂足是M,
则tan∠MPB=
| ||
| 1 |
| 3T |
| 4 |
| ||
| 1 |
| T |
| 4 |
∴tan∠APB=tan(∠MPB-∠MPA)=
| tan∠MPB-tan∠MPA |
| 1+tan∠MPB•tan∠MPA |
=
| ||||
1+
|
| 1 |
| 2 |
解得:T=4或T=
| 4 |
| 3 |
∵f(x)=sin[ωπ(x+
| 1 |
| 3 |
| 1 |
| 3 |
∴
| 2π |
| ωπ |
| 2π |
| ωπ |
| 4 |
| 3 |
| 1 |
| 2 |
| 3 |
| 2 |
∴f(x)=sin(
| 1 |
| 2 |
| 1 |
| 6 |
| 3 |
| 2 |
| 1 |
| 2 |
(2)当f(x)=sin(
| 1 |
| 2 |
| 1 |
| 6 |
由f(
| 2 |
| π |
| 1 |
| 3 |
| 2 |
| π |
| 1 |
| 3 |
2
| ||
| 3 |
sin[
| 1 |
| 2 |
| 2 |
| π |
| 1 |
| 3 |
| 1 |
| 6π |
| 1 |
| 2 |
| 2 |
| π |
| 1 |
| 3 |
| 1 |
| 6 |
2
| ||
| 3 |
即sinα•sinβ=
2
| ||
| 3 |
| 1 |
| 2 |
2
| ||
| 3 |
由α+β=
| 3π |
| 4 |
5
| ||
| 6 |
当f(x)=sin(
| 3 |
| 2 |
| 1 |
| 2 |
由f(
| 2 |
| π |
| 1 |
| 3 |
| 2 |
| π |
| 1 |
| 3 |
2
| ||
| 3 |
sin[
| 3 |
| 2 |
| 2 |
| π |
| 1 |
| 3 |
| π |
| 2 |
| 3 |
| 2 |
| 2 |
| π |
| 1 |
| 3 |
| π |
| 2 |
2
| ||
| 3 |
即sin3α•sin3β=
2
| ||
| 3 |
| 1 |
| 2 |
2
| ||
| 3 |
由α+β=
| 3π |
| 4 |
11
| ||
| 6 |
∴
| sin(θ+α)sin(θ+β) |
| cos2θ |
点评:本题考查了由三角函数的部分图象求函数的解析式,考查了三角函数的求值,考查了三角函数的有界性,是中档题.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
函数f(x)=
的图象关于( )
| ||
| x |
| A、x轴对称 | B、原点对称 |
| C、y轴对称 | D、直线y=x对称 |
函数f(x)=ax+loga(x+1)在x∈[0,1]上的最大值与最小值的和为a,则a=( )
A、
| ||
B、
| ||
| C、2 | ||
| D、4 |
 某人准备用长为m的不锈钢材料做成下部为矩形、上部为半圆形的艺术窗框,如图,试问如何设计,可以使得窗框围成的面积最大,以取得最佳的采光效果.
某人准备用长为m的不锈钢材料做成下部为矩形、上部为半圆形的艺术窗框,如图,试问如何设计,可以使得窗框围成的面积最大,以取得最佳的采光效果.