题目内容
19．在等差数列{an}中，已知a4=10，a8=18，求a10及前10项的和S10．分析 设出等差数列的公差，由已知求得公差，进一步求得首项，然后分别利用通项公式及前n项和公式求得答案．
解答 解：设等差数列{an}的公差为d，
由a4=10，a8=18，得$d=\frac{{a}_{8}-{a}_{4}}{8-4}=\frac{18-10}{4}=2$，
∴a1=a4-3d=10-6=4．
∴a10=a1+9d=4+18=22；
${S}_{10}=10×4+\frac{10×9×2}{2}=130$．
点评 本题考查等差数列的性质，考查了等差数列的前n项和，是基础的计算题．
练习册系列答案
阅读快车系列答案
相关题目
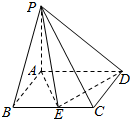如图，四棱锥P-ABCD的底面ABCD是平行四边形，且PA⊥底面ABCD，AB=2，PA=BC=4，∠ABC=60°，点E是线段BC（包括端点）上的动点．
10．若复数z满足$i•z=-\frac{1}{2}（1+i）$，则z的共轭复数的虚部是（ ）
| A． | $-\frac{1}{2}i$ | B． | $\frac{1}{2}i$ | C． | $-\frac{1}{2}$ | D． | $\frac{1}{2}$ |
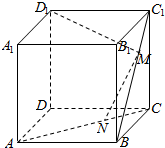如图，正方体ABCD-A1B1C1D1的棱长为a，$\frac{AN}{NC}=\frac{BM}{{M{C_1}}}=3$．
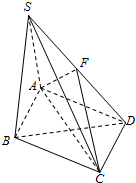如图，在四棱锥S-ABCD中，底面ABCD是菱形，∠BAD=60°，侧面SAB⊥底面ABCD，并且SA=SB=AB=2，F为SD的中点．