题目内容
11.设命题P:?x∈R,x2-2x>a,命题Q:?x0∈R,x02+2ax0+2-a=0,如果“P或Q”为真,“P且Q”为假,a的取值范围(-2,-1)∪[1,+∞).分析 求出命题的等价条件,利用复合命题真假关系进行判断即可.
解答 解:x2-2x=(x-1)2-1≥-1,
若:?x∈R,x2-2x>a,则a<-1,
若:?x0∈R,x02+2ax0+2-a=0,
则判别式△=4a2-4(2-a)≥0,
即a2+a-2≥0,解得a≥1或a≤-2,
若“P或Q”为真,“P且Q”为假,
则P,Q一真一假,
若P真,Q假,则$\left\{\begin{array}{l}{a<-1}\\{-2<a<1}\end{array}\right.$,即-2<a<-1,
若P假,Q真,则$\left\{\begin{array}{l}{a≥1或a≤-2}\\{a≥-1}\end{array}\right.$,即a≥1,
故实数a的取值范围是(-2,-1)∪[1,+∞),
故答案为:(-2,-1)∪[1,+∞)
点评 本题主要考查复合命题的应用,根据函数性质求出命题P,Q的等价条件是解决本题的关键.

练习册系列答案
相关题目
16.下列函数既是偶函数,又在(0,+∞)上单调递增的是( )
| A. | y=-x2 | B. | y=x3 | C. | y=log2|x| | D. | y=-3-x |
3.一个年级共有12个班,每个班学生的学号从1到50,为交流学习经验,要求每班学号为14的同学留下,这里运用的是( )
| A. | 分层抽样法 | B. | 抽签法 | C. | 随机数表法 | D. | 系统抽样法 |
20.设U={1,2,3,4},M={2,3},N={2,3,4},则(∁UM)∩N=( )
| A. | {1,4} | B. | {2,3} | C. | {4} | D. | {2,4} |
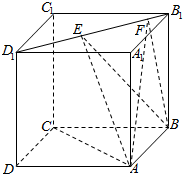 如图,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E,F,且EF=$\frac{\sqrt{2}}{2}$,则下列结论中错误的个数是( )
如图,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E,F,且EF=$\frac{\sqrt{2}}{2}$,则下列结论中错误的个数是( )