题目内容
7.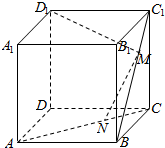 如图,正方体ABCD-A1B1C1D1的棱长为a,$\frac{AN}{NC}=\frac{BM}{{M{C_1}}}=3$.
如图,正方体ABCD-A1B1C1D1的棱长为a,$\frac{AN}{NC}=\frac{BM}{{M{C_1}}}=3$.(Ⅰ)求MN的长;
(Ⅱ)求异面直线D1M与AC所成角的余弦值.
分析 (Ⅰ)分别以DA,DC,DD1为x轴,y轴,z轴,建立空间直角坐标系O-xyz,利用向量法能求出|MN|的长.
(Ⅱ)分另求出$\overrightarrow{{D_1}M}=(\frac{a}{4},\frac{3a}{4},-a)$,$\overrightarrow{AC}=(-a,a,0)$,利用向量法能求出异面直线D1M与AC所成角的余弦值.
解答 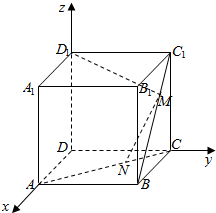 解:(Ⅰ)分别以DA,DC,DD1为x轴,y轴,z轴,建立空间直角坐标系O-xyz,
解:(Ⅰ)分别以DA,DC,DD1为x轴,y轴,z轴,建立空间直角坐标系O-xyz,
则$M(\frac{a}{4},\frac{3a}{4},0),N(\frac{a}{4},a,\frac{3a}{4})$,…2分
∴|MN|=$\sqrt{(\frac{a}{4}-\frac{a}{4})^{2}+(a-\frac{3a}{4})^{2}+(\frac{3a}{4}-a)^{2}}$=$\frac{\sqrt{10}a}{4}$.…2分
(Ⅱ)D1(0,0,a),A(a,0,0),C(0,a,0),
$\overrightarrow{{D_1}M}=(\frac{a}{4},\frac{3a}{4},-a)$,$\overrightarrow{AC}=(-a,a,0)$,
$cos<\overrightarrow{{D_1}M},\overrightarrow{AC}>$=$\frac{\overrightarrow{{D}_{1}M}•\overrightarrow{AC}}{|\overrightarrow{{D}_{1}M}|•|\overrightarrow{AC}|}$=$\frac{-\frac{{a}^{2}}{4}+\frac{3{a}^{2}}{4}}{\sqrt{\frac{26{a}^{2}}{16}}•\sqrt{2}a}$=$\frac{\sqrt{13}}{13}$.…3分
所以异面直线D1M与AC所成角的余弦值$\frac{\sqrt{13}}{13}$.…1分
点评 本题考查线段长的求法,考查异面直线所成角的求法,是中档题,解题时要认真审题,注意向量法的合理运用.

 考前必练系列答案
考前必练系列答案| A. | $\frac{1}{27}$ | B. | $-\frac{1}{27}$ | C. | ±$\frac{1}{27}$ | D. | $\frac{1}{3}$ |
| A. | y=-x2 | B. | y=x3 | C. | y=log2|x| | D. | y=-3-x |
 且
且 是单调增函数;命题
是单调增函数;命题 ,
, .则下列命题为真命题的是( )
.则下列命题为真命题的是( ) B.
B. C.
C. D.
D.
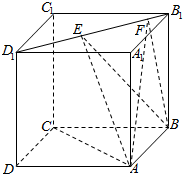 如图,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E,F,且EF=$\frac{\sqrt{2}}{2}$,则下列结论中错误的个数是( )
如图,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E,F,且EF=$\frac{\sqrt{2}}{2}$,则下列结论中错误的个数是( )