题目内容
4.在等差数列{an}中,a1+a2=5,a3=7,记数列{$\frac{1}{{a}_{n}{a}_{n+1}}$}的前n项和为Sn.(1)求数列{an}的通项公式;
(2)求Sn,求证:Sn≤$\frac{1}{3}$;
(3)是否存在正整数m、n,且1<m<n,使得1、Sm、Sn成等比数列?若存在,求出所有符合条件的m、n的值;若不存在,请说明理由.
分析 (1)利用等差数列的通项公式即可得出;
(2)利用“裂项求和”与“放缩法”即可得出;
(3)假设存在正整数m、n,且1<m<n,使得S1、Sm、Sn成等比数列,可得:${S_m}^2={S_1}{S_n}$.$n=\frac{{4{m^2}}}{{-3{m^2}+6m+1}}$.利用-3m2+6m+1>0.解得m,即可得出.
解答 (1)解:设等差数列{an}的公差为d,
∵$\left\{\begin{array}{l}{a_1}+{a_2}=5\\{a_3}=7.\end{array}\right.$,即$\left\{\begin{array}{l}2{a_1}+d=5\\{a_1}+2d=7.\end{array}\right.$,解得$\left\{\begin{array}{l}{a_1}=1\\ d=3.\end{array}\right.$,
∴an=1+3(n-1)=3n-2.
∴数列{an}的通项为an=3n-2(n∈N*).
(2)证明:∵$\frac{1}{{{a_n}{a_{n+1}}}}=\frac{1}{{({3n-2})({3n+1})}}=\frac{1}{3}({\frac{1}{3n-2}-\frac{1}{3n+1}})$,
∴数列$\left\{{\frac{1}{{{a_n}{a_{n+1}}}}}\right\}$的前n项和${S_n}=\frac{1}{{{a_1}{a_2}}}+\frac{1}{{{a_2}{a_3}}}+\frac{1}{{{a_3}{a_4}}}+…+\frac{1}{{{a_{n-1}}{a_n}}}+\frac{1}{{{a_n}{a_{n+1}}}}$
=$\frac{1}{3}({1-\frac{1}{4}})+\frac{1}{3}({\frac{1}{4}-\frac{1}{7}})+\frac{1}{3}({\frac{1}{7}-\frac{1}{10}})+…+\frac{1}{3}({\frac{1}{3n-5}-\frac{1}{3n-2}})+\frac{1}{3}({\frac{1}{3n-2}-\frac{1}{3n+1}})$
=$\frac{1}{3}({1-\frac{1}{3n+1}})=\frac{n}{3n+1}≤\frac{1}{3}$.
(3)解:假设存在正整数m、n,且1<m<n,使得S1、Sm、Sn成等比数列,
则${S_m}^2={S_1}{S_n}$.即${({\frac{m}{3m+1}})^2}=\frac{1}{4}×\frac{n}{3n+1}$.
∴$n=\frac{{4{m^2}}}{{-3{m^2}+6m+1}}$.
∵n>0,∴-3m2+6m+1>0.即3m2-6m-1<0.
∵m>1,∴$1<m<1+\frac{{2\sqrt{3}}}{3}<3$.
∵m∈N*,∴m=2.
此时$n=\frac{{4{m^2}}}{{-3{m^2}+6m+1}}=16$.
∴存在满足题意的正整数m、n,且只有一组解,即m=2,n=16.
点评 本题考查了等差数列与等比数列的通项公式、“裂项求和”方法、不等式的解法及其性质,考查了推理能力与计算能力,属于中档题.

 金钥匙试卷系列答案
金钥匙试卷系列答案| A. | y=-x2 | B. | y=x3 | C. | y=log2|x| | D. | y=-3-x |
| A. | $y={x^{\frac{2}{3}}}$ | B. | $y={x^{\frac{3}{2}}}$ | C. | y=x-2 | D. | $y={x^{-\frac{1}{2}}}$ |
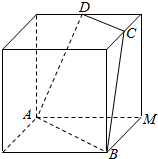 如图所示,正方体的棱长为2,C、D分别是两条棱的中点,A、B、M是顶点,那么M到截面ABCD的距离是$\frac{4}{3}$.
如图所示,正方体的棱长为2,C、D分别是两条棱的中点,A、B、M是顶点,那么M到截面ABCD的距离是$\frac{4}{3}$.