若复数z满足$i•z=-\frac{1}{2}(1+i)$.则z的共轭复数的虚部是( )A．$-\frac{1}{2}i$B．$\frac{1}{2}i$C．$-\frac{1}{2}$D．$\frac{1}{2}$ 题目和参考答案——青夏教育精英家教网—

题目内容

10．若复数z满足$i•z=-\frac{1}{2}（1+i）$，则z的共轭复数的虚部是（　　）

A．

$-\frac{1}{2}i$

B．

$\frac{1}{2}i$

C．

$-\frac{1}{2}$

D．

$\frac{1}{2}$

分析利用复数的运算法则、共轭复数的定义即可得出．

解答解：满足$i•z=-\frac{1}{2}（1+i）$，∴-i•$i•z=-\frac{1}{2}（1+i）$（-i），
∴z=$\frac{1}{2}（i-1）$，
∴$\overline{z}$=$-\frac{1}{2}-\frac{1}{2}$i．
则z的共轭复数的虚部是$-\frac{1}{2}$．
故选：C．

点评本题考查了复数的运算法则、共轭复数的定义，考查了计算能力，属于基础题．

练习册系列答案

决胜新中考学霸宝典系列答案

天利38套常考基础题系列答案

智乐文化中考全真模拟试卷尖子生热身用系列答案

相关题目

已知函数．

（1）若函数在定义域上是单调增函数，求的最小值；

（2）若方程在区间上有两个不同的实根，求的取值范围．

1．已知|$\overrightarrow{a}$|=2，|$\overrightarrow{b}$|=1，$\overrightarrow{a}和\overrightarrow{b}$的夹角为$\frac{π}{3}$，则$\overrightarrow{a}•\overrightarrow{b}$=1．

18．已知等比数列{a_n}，a₁=1，a₅=$\frac{1}{9}$，则a₂a₃a₄（　　）

5．若直线l₁：y=kx+1与l₂：x-y-1=0的交点在第一象限内，则k的取值范围是（-1，1）．

15．已知函数f（x）是定义在（-∞，+∞）上的偶函数，且在[0，+∞）上是增函数，若实数a满足：$f（{log_3}a）+f（{log_3}\frac{1}{a}）≤2f（1）$，则a的取值范围是$\frac{1}{3}$≤a≤3．

2．

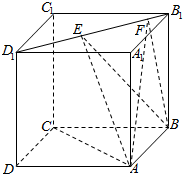如图，正方体ABCD-A₁B₁C₁D₁的棱长为1，线段B₁D₁上有两个动点E，F，且EF=$\frac{\sqrt{2}}{2}$，则下列结论中错误的个数是（　　）
（1）AC⊥BE；
（2）若P为AA₁上的一点，则P到平面BEF的距离为$\frac{\sqrt{2}}{2}$；
（3）三棱锥A-BEF的体积为定值；
（4）在空间与三条直线DD₁，AB，B₁C₁都相交的直线有无数条．

19．在等差数列{a_n}中，已知a₄=10，a₈=18，求a₁₀及前10项的和S₁₀．

20．设U={1，2，3，4}，M={2，3}，N={2，3，4}，则（∁_UM）∩N=（　　）