题目内容
如图,直线l1:ax-y+b=0与直线l2:bx+y-a=0,(ab≠0)的图象应是( )
A、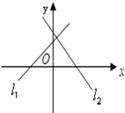 |
B、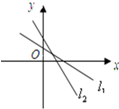 |
C、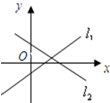 |
D、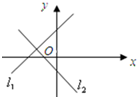 |
考点:直线的一般式方程
专题:直线与圆
分析:把二直线的方程化为斜截式,先假设其中一条直线正确,看另一条直线的斜率和截距是否符合即可.
解答:
解:直线l1的方程是ax-y+b=0,可化为y=ax+b,l2的方程是bx+y-a=0,可化为y=-bx+a(ab≠0).
A中,假设直线l1正确:即斜率a>0,在y轴上的截距b>0.则图中直线l2的斜率-b<0,且y轴上的截距是a>0.符合条件,∴正确.
B中,假设直线l1正确:即斜率a<0,在y轴上的截距b>0.则图中直线l2的斜率-b<0,且y轴上的截距是a>0.与a<0矛盾,∴错误.
C中,假设直线l1正确:即斜率a>0,在y轴上的截距b<0.则图中直线l2的斜率-b<0,与b<0矛盾,∴错误.
D中,假设直线l1正确:即斜率a>0,在y轴上的截距b>0.则图中直线l2的斜率-b<0,且y轴上的截距是a<0.与a<0矛盾,∴错误.
图象正确的应该是A.
故选:A.
A中,假设直线l1正确:即斜率a>0,在y轴上的截距b>0.则图中直线l2的斜率-b<0,且y轴上的截距是a>0.符合条件,∴正确.
B中,假设直线l1正确:即斜率a<0,在y轴上的截距b>0.则图中直线l2的斜率-b<0,且y轴上的截距是a>0.与a<0矛盾,∴错误.
C中,假设直线l1正确:即斜率a>0,在y轴上的截距b<0.则图中直线l2的斜率-b<0,与b<0矛盾,∴错误.
D中,假设直线l1正确:即斜率a>0,在y轴上的截距b>0.则图中直线l2的斜率-b<0,且y轴上的截距是a<0.与a<0矛盾,∴错误.
图象正确的应该是A.
故选:A.
点评:本题考查了由图象判定直线方程的问题,正确理解直线的斜率和截距是解题的关键.

练习册系列答案
相关题目
以A(-1,2 ),B(5,6)为直径端点的圆的方程是( )
| A、(x-2)2+(y-4)2=13 |
| B、(x-2)2+(y+4)2=13 |
| C、(x+2)2+(y-4)2=13 |
| D、(x+2)2+(y+4)2=13 |
已知sin(
+x)=
,则sin2x的值为( )
| π |
| 4 |
| 3 |
| 5 |
A、
| ||
B、-
| ||
C、-
| ||
D、
|
在等比数列{an}中,Sn表示前n项和,若a3=2S2+1,a4=2S3+1,则公比q=( )
| A、-3 | B、-1 | C、3 | D、1 |
点P(tan2013°,cos2013°)位于( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |