题目内容
已知cosα=
，α∈（0，
）
（1）求tanα的值；
（2）求sin2α的值．
| 1 |
| 2 |
| π |
| 2 |
（1）求tanα的值；
（2）求sin2α的值．
考点：二倍角的正弦,同角三角函数间的基本关系
专题：三角函数的求值
分析：（1）先根据α的范围求得sinα的值，进而根据同角三角函数基本关系求得tanα的值．
（2）利用二倍角公式求得sin2α的值．
（2）利用二倍角公式求得sin2α的值．
解答：
解：（1）∵α∈（0，
）
∴sinα=
=
，
∴tanα=
=
（2）sin2α=2sinαcosα=
．
| π |
| 2 |
∴sinα=
1-
|
| ||
| 2 |
∴tanα=
| sinα |
| cosα |
| 3 |
（2）sin2α=2sinαcosα=
| ||
| 2 |
点评：本题主要考查了二倍角公式的应用，同角三角函数基本关系的应用．本题也可根据cosα=
求得α的值，直接求得tanα和sin2α的值．
| 1 |
| 2 |
练习册系列答案
海淀课时新作业金榜卷系列答案
期末金牌卷系列答案
轻松课堂标准练系列答案
相关题目
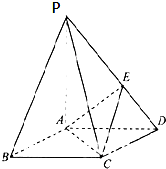如图，在底面为菱形的四棱锥P-ABCD中，∠ABC=60°，PA=AC=1，PB=PD=
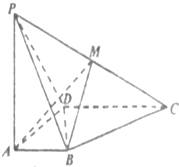如图所示，四棱锥P-ABCD中，AB⊥AD，CD⊥AD，PA⊥底面ABCD，PA=AD=CD=2AB=2，M为PC的中点．
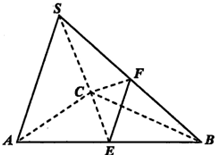在三棱锥S-ABC中，△ABC是边长为2的正三角形，平面SAC⊥平面ABC，
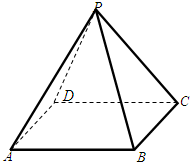在正四棱锥P-ABCD中，PA=2，直线PA与平面ABCD所成的角为60°．