题目内容
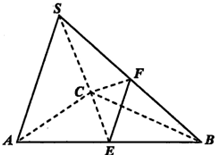在三棱锥S-ABC中，△ABC是边长为2的正三角形，平面SAC⊥平面ABC，SA=SC=| 3 |
（1）证明：AC⊥SB；
（2）求锐二面角F-CE-B的余弦值．
考点：二面角的平面角及求法,直线与平面垂直的性质
专题：空间位置关系与距离,空间角
分析：（1）根据线面垂直的性质，证明AC⊥平面SOB，即可证明AC⊥SB；
（2）求出二面角的平面角，根据三角形的边角关系，即可求锐二面角F-CE-B的余弦值．
（2）求出二面角的平面角，根据三角形的边角关系，即可求锐二面角F-CE-B的余弦值．
解答：
（1）证明：取AC中点O，连结SO，BO．
∵SA=SC，AB=AC，∴AC⊥SO且AC⊥BO，
∴AC⊥平面SOB，又SB?平面SOB，∴AC⊥SB．
（2）设OB与CE交于点G，取OB中点为M，作MH⊥CE交CE于点H，连结FM，FG．
∵平面SAC⊥平面ABC且AC⊥SO，
∴SO⊥平面ABC，
∵SO∥FM，∴FM⊥平面BCE，∴FM⊥CE，
从而CE⊥平面FMH．∴CE⊥FH，
∴∠FHM是二面角F-CE-B的平面角．
由△GHM∽△GEB得HM=
，
在Rt△FMH中FM=
，FH=
，
∴cos∠FHM=
=
，
故锐二面角F-CE-B的余弦值为
．
∵SA=SC，AB=AC，∴AC⊥SO且AC⊥BO，
∴AC⊥平面SOB，又SB?平面SOB，∴AC⊥SB．
（2）设OB与CE交于点G，取OB中点为M，作MH⊥CE交CE于点H，连结FM，FG．
∵平面SAC⊥平面ABC且AC⊥SO，
∴SO⊥平面ABC，
∵SO∥FM，∴FM⊥平面BCE，∴FM⊥CE，
从而CE⊥平面FMH．∴CE⊥FH，
∴∠FHM是二面角F-CE-B的平面角．
由△GHM∽△GEB得HM=
| 1 |
| 4 |
在Rt△FMH中FM=
| ||
| 2 |
| 3 |
| 4 |
∴cos∠FHM=
| HM |
| FH |
| 1 |
| 3 |
故锐二面角F-CE-B的余弦值为
| 1 |
| 3 |
点评：本题主要考查面面垂直的性质，以及二面角的求解，根据对应求出二面角的平面角是解决本题的关键．
练习册系列答案
小学期末标准试卷系列答案
相关题目