题目内容
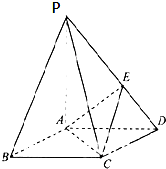 如图,在底面为菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=1,PB=PD=
如图,在底面为菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=1,PB=PD=| 2 |
(Ⅰ)求证:PA⊥平面ABCD;
(Ⅱ)求二面角E-AC-D的正弦值;
(Ⅲ)在棱PC上是否存在一点F,使得BF∥平面EAC?若存在,试求出PF的值:若不存在,请说明理由.
考点:用空间向量求平面间的夹角,直线与平面平行的判定,直线与平面垂直的判定
专题:转化思想,空间位置关系与距离,空间角
分析:(1)要证PA⊥平面ABCD,只需PA垂直于平面ABCD内的两条相交直线,根据题目中给的线段长,将PA,AB,PB放在一个三角形PAB中,经计算可知PA⊥AB,同理可证PA⊥AD,第一问迎刃而解;
(2)据第(1)问结果,可以以A点为原点建立适当的坐标系,然后通过设点、求直线方向向量,平面法向量,最终将二面角转化为法向量的夹角问题;
(3)先假设存在点F,然后利用“BF∥平面EAC”构造等量关系(如平面法向量与直线方向向量共线列方程),若方程有解,则存在,否则不存在.
(2)据第(1)问结果,可以以A点为原点建立适当的坐标系,然后通过设点、求直线方向向量,平面法向量,最终将二面角转化为法向量的夹角问题;
(3)先假设存在点F,然后利用“BF∥平面EAC”构造等量关系(如平面法向量与直线方向向量共线列方程),若方程有解,则存在,否则不存在.
解答:
解:(Ⅰ)证明:∵底面ABCD为菱形,∠ABC=60°
∴AB=AD=AC=1,
∵在△PAB中,PA=AB=1,PB=
,
∴PA2+AB2=PB2,
∴PA⊥AB
同理,在△PAD中,可证PA⊥AD,
∵AB∩AD=A
∴PA⊥平面ABCD.
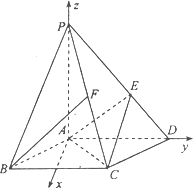
(Ⅱ)以A为原点,过A点垂直于平面PAD的直线为x轴,直线AD、AP分别为y、z轴建立空间直角坐标系,
如图,则A(0,0,0),B(
,-
,0),C(
,
,0),D(0,1,0),P(0,0,1),E(0,
,
),
则
=(
,
,0),
=(0,
,
),
设平面EAC的法向量为
=(x,y,z),
由
得
,
令x=1,则y=-
,z=2
,故
=(1,-
,2
),
易知,平面DAC的法向量为
=(0,0,1),
设二面角E-AC-D的大小为θ(θ为锐角),
由cosθ=|cos<
,
>|=
,得
cosθ=
=
,故sinθ=
.
(Ⅲ)设点F是棱PC上的一点,
且
=λ
=(
λ,
λ,-λ),其中0<λ<1,
又
=(-
,
,1),则
=(
λ-
,
λ+
,-λ+1),
由(Ⅱ)可知,平面EAC的法向量为
=(1,-
,2
),
要使BF∥面EAC,需满足
⊥
,则
•
=0,
∴
λ-
-
λ-
-2
λ+2
=0,
解得λ=
,故F为棱PC的中点时,
∥面EAC,
此时F(
,
,
),
=(
,
,-
),
∴PF的值为|
|=
=
.
∴AB=AD=AC=1,
∵在△PAB中,PA=AB=1,PB=
| 2 |
∴PA2+AB2=PB2,
∴PA⊥AB
同理,在△PAD中,可证PA⊥AD,
∵AB∩AD=A
∴PA⊥平面ABCD.
(Ⅱ)以A为原点,过A点垂直于平面PAD的直线为x轴,直线AD、AP分别为y、z轴建立空间直角坐标系,
如图,则A(0,0,0),B(
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 3 |
则
| AC |
| ||
| 2 |
| 1 |
| 2 |
| AE |
| 2 |
| 3 |
| 1 |
| 3 |
设平面EAC的法向量为
| n |
由
|
|
令x=1,则y=-
| 3 |
| 3 |
| n |
| 3 |
| 3 |
易知,平面DAC的法向量为
| m |
设二面角E-AC-D的大小为θ(θ为锐角),
由cosθ=|cos<
| m |
| n |
|
| ||||
|
|
cosθ=
2
| ||
| 4×1 |
| ||
| 2 |
| 1 |
| 2 |

(Ⅲ)设点F是棱PC上的一点,
且
| PF |
| PC |
| ||
| 2 |
| 1 |
| 2 |
又
| BP |
| ||
| 2 |
| 1 |
| 2 |
| BF |
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
由(Ⅱ)可知,平面EAC的法向量为
| n |
| 3 |
| 3 |
要使BF∥面EAC,需满足
| BF |
| n |
| BF |
| n |
∴
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| 3 |
| 3 |
解得λ=
| 1 |
| 2 |
| BF |
此时F(
| ||
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
| PF |
| ||
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
∴PF的值为|
| PF |
|
| ||
| 2 |
点评:空间中的垂直与平行主要是线线、线面、面面间的平行与垂直关系的互相转化,只要熟练掌握有关的定理、推论和相应的方法,就能解决问题,当然如果可以建立空间直角坐标系,也可以借助于直线的方向向量和平面的法向量进行证明;二面角一般转化为两平面的法向量的夹角,注意判断二面角是钝角还是锐角;探究性问题一般是先假设结论成立,然后将结论当成条件结合已知构造方程或不等式求解,若有解,则存在,否则不存在.

练习册系列答案
相关题目
已知sin4•tan7的值( )
| A、不大于0 | B、大于0 |
| C、不小于0 | D、小于0 |