题目内容
4.F1(-4,0)、F2(4,0)为两个定点,P为动点,若|PF1|+|PF2|=8,则动点P的轨迹为( )| A. | 椭圆 | B. | 直线 | C. | 射线 | D. | 线段 |
分析 利用:|PF1|+|PF2|=|F1F2|,即可得出动点P的轨迹.
解答 解:F1,F2为平面上两个不同定点,|F1F2|=8,
动点P满足:|PF1|+|PF2|=8,
则动点P的轨迹是以F1,F2为端点的线段.
故选:D.
点评 本题考查了轨迹方程,解答的关键是对题意的理解,是基础题.

练习册系列答案
相关题目
12.若实数a、b、c满足3a=4b=6c,则下列等式成立的是( )
| A. | $\frac{1}{a}+\frac{1}{b}$=$\frac{1}{c}$ | B. | $\frac{2}{a}+\frac{1}{b}$=$\frac{2}{c}$ | C. | $\frac{1}{a}+\frac{2}{b}$=$\frac{1}{c}$ | D. | $\frac{1}{a}+\frac{1}{b}$=$\frac{2}{c}$ |
19.如果集合P={x|x>-1},那么( )
| A. | 0⊆P | B. | {0}∈P | C. | ∅∈P | D. | {0}?P |
8.已知f(x)=lg($\sqrt{{x}^{2}+1}$-ax)是一个奇函数,则实数a的值是( )
| A. | 1 | B. | -1 | C. | ±1 | D. | 10 |
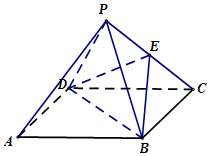 如图,在正四棱锥P-ABCD中,PA=AB=a,E是棱PC的中点.
如图,在正四棱锥P-ABCD中,PA=AB=a,E是棱PC的中点.