题目内容
6. 已知函数f(x)=x2-2x-1,x∈(-1,2].
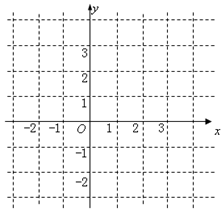
已知函数f(x)=x2-2x-1,x∈(-1,2].(Ⅰ)画出函数f(x)的图象;
(Ⅱ)讨论当实数k为何实数值时,方程x2-2x-1-k=0在(-1,2]上的解集为空集、单元素集、两元素集?
分析 (Ⅰ)直接在坐标系中画出函数f(x)的图象;
(Ⅱ)利用函数的图象,直接判断y=k与f(x)=x2-2x-1交点个数,写出结果即可.
解答  (本题12分)
(本题12分)
解:(Ⅰ)函数f(x)=x2-2x-1,x∈(-1,2].
(注意端点.)
(Ⅱ)x2-2x-1-k=0,即x2-2x-1=k,作y=k的图象.
当k≥2,或k<-2时,解集为空集;
当-1<k<2,或k=-2时,解集为单元素集;
当-2<k≤-1时,解集为两元素集.
点评 本题考查三角函数的图象与性质,考查数形结合以及计算能力.

练习册系列答案
相关题目
17.设f(x)与g(x)是定义在同一区间[a,b]上的两个函数,若函数y=f(x)-g(x)在x∈[a,b]上有两个不同的零点,则称f(x)和g(x)在[a,b]上是“关联函数”,区间[a,b]称为“关联区间”.若f(x)=x2-3x+1与g(x)=x+m在[0,3]上是“关联函数”,则m的取值范围为( )
| A. | (-3,+∞) | B. | (-3,-2] | C. | [-3,0] | D. | [-2,1] |
15.若全集U={x∈N|1≤x≤7},集合A={1,2,3,5},B={2,3,4},则集合CUA∩CUB等于( )
| A. | { 2,3 } | B. | { 1,5,6,7 } | C. | { 6,7 } | D. | { 1,5 } |
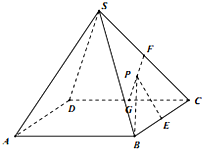 如图,正四棱锥S-ABCD中.SA=AB=2,E、F、G分别为BC、SC、DC的中点,设P为线段FG上任意一点.
如图,正四棱锥S-ABCD中.SA=AB=2,E、F、G分别为BC、SC、DC的中点,设P为线段FG上任意一点.