题目内容
判断函数f（x）=x|x|+x3的奇偶性．
考点：函数奇偶性的判断
专题：函数的性质及应用
分析：根据奇偶性的定义，判断f（-x）与f（x）之间的关系，即可判断函数f（x）的奇偶性；
解答：
解：函数f（x）=x|x|+x3的定义域为R，
∵f（-x）=-x|-x|+（-x）3=-x|x|-x3=-f（x），
故函数f（x）=x|x|+x3为奇函数．
∵f（-x）=-x|-x|+（-x）3=-x|x|-x3=-f（x），
故函数f（x）=x|x|+x3为奇函数．
点评：此题主要考查函数的奇偶性，解题的关键是利用定义进行判断，是一道基础题．
练习册系列答案
相关题目
已知f（x）=ax3+2x2+1，若f′（-1）=4，则a=（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
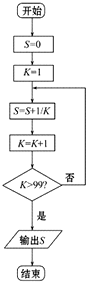给出一个算法的程序框图（如图所示）．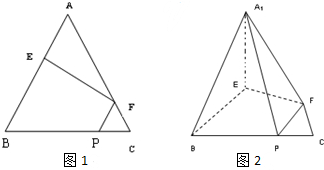
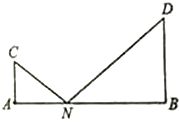如图，C，D是两个小区的所在地，C，D到一条公路AB的垂直距离CA=1km，DB=2km，AB两端之间的距离为4km，某公交公司将在AB之间找一点N，在N处建造一个公交站台．