题目内容
已知x∈（b，a）且x≠0，
∈（
，
），则实数a，b满足（ ）
| 1 |
| x |
| 1 |
| a |
| 1 |
| b |
| A、a＜b＜0 |
| B、a＜0＜b |
| C、a＞0＞b |
| D、a＞b＞0 |
考点：区间与无穷的概念
专题：不等式的解法及应用
分析：根据区间表示时，左边数小于右边，可得b＜a，且
＜
，结合不等式的基本性质可得ab＞0，即a，b同号，比照后可得答案．
| 1 |
| a |
| 1 |
| b |
解答：
解：∵x∈（b，a），
∴b＜a，
∵
∈（
，
），
∴
＜
，
即ab＞0，即a，b同号，
故b＜a＜0，或0＜b＜a，
故选：D
∴b＜a，
∵
| 1 |
| x |
| 1 |
| a |
| 1 |
| b |
∴
| 1 |
| a |
| 1 |
| b |
即ab＞0，即a，b同号，
故b＜a＜0，或0＜b＜a，
故选：D
点评：本题考查的知识点是区间的概念，不等式的基本性质，难度不大，属于基础题．
练习册系列答案
相关题目
若函数y=f（x）在R上单调递增，且f（m2+1）＞f（-m+1），则实数m的取值范围是（ ）
| A、（-∞，-1） |
| B、（0，+∞） |
| C、（-1，0） |
| D、（-∞，-1）∪（0，+∞） |
已知a=log34，b=0.910，c=log20.8，则有（ ）
| A、a＞b＞c |
| B、b＞a＞c |
| C、c＞a＞d |
| D、b＞c＞a |
函数f（x）=x2-6x+1的零点个数是（ ）
| A、0 | B、1 | C、2 | D、3 |
观察下列式子：1+
＜
，1+
+
＜
，1+
+
+
＜
，…，根据以上式子可以猜想：1+
+
+…+
＜（ ）
| 1 |
| 22 |
| 3 |
| 2 |
| 1 |
| 22 |
| 1 |
| 32 |
| 5 |
| 3 |
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| 42 |
| 7 |
| 4 |
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| 20142 |
A、
| ||
B、
| ||
C、
| ||
D、
|
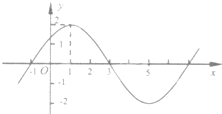已知函数f（x）=Asin（ωx+φ），（A＞0，ω＞0，|φ|＜