题目内容
已知向量
=(x+z,3),
=(2,y-z),且
⊥
.若x,y满足不等式|x|+|y|≤1,则z的取值范围为 .
| a |
| b |
| a |
| b |
考点:数量积判断两个平面向量的垂直关系
专题:平面向量及应用
分析:根据平面向量的垂直的坐标运算法则,由已知
=(x+z,3),
=(2,y-z),且
⊥
,得到关于x,y,z的方程,即关于Z的目标函数,画出约束条x+y≤1对应的平面区域,并求出各个角点的坐标,代入即可求出目标函数的最值,进而给出z的取值范围.
| a |
| b |
| a |
| b |
解答:
 解:∵
解:∵
=(x+z,3),
=(2,y-z),且
⊥
,
∴(x+z)×2+3×(y-z)=2x+3y-z=0,
即z=2x+3y,
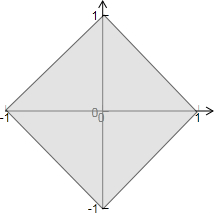
∵满足不等式|x|+|y|≤1的平面区域如下图所示:
由图可知当x=0,y=1时,z取最大值3,
当x=0,y=-1时,z取最小值-3,
故z的取值范围为[-3,3];
故答案为[-3,3].
 解:∵
解:∵| a |
| b |
| a |
| b |
∴(x+z)×2+3×(y-z)=2x+3y-z=0,
即z=2x+3y,
∵满足不等式|x|+|y|≤1的平面区域如下图所示:
由图可知当x=0,y=1时,z取最大值3,
当x=0,y=-1时,z取最小值-3,
故z的取值范围为[-3,3];
故答案为[-3,3].
点评:本题考查了两个平面向量的垂直性质,简单线性规划的应用,其中利用平面向量的垂直的坐标运算法则,求出目标函数的解析式是解答本题的关键.

练习册系列答案
相关题目
空间直角坐标系O-xyz中,已知点B是点A(3,7,-4)在xOz平面上的射影,则
2等于( )
| OB |
| A、(9,0,16) | B、25 |
| C、5 | D、13 |
若0>m>n,则下列结论正确的是( )
| A、2m<2n | ||||
B、m+
| ||||
C、log
| ||||
| D、m2<n2 |
在区间[-3,4]上随机地取一个实数a,使得二次方程x2+2ax-2a+3=0有实根的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|