题目内容
18.数列{an}的前n项和为Sn,若${a_1}=1,{S_n}=3{a_{n+1}}({n∈{N^*}}),则{S_n}$=$(\frac{4}{3})^{n-1}$.分析 由已知数列递推式可得Sn-1=3an(n≥2),与圆递推式作差可得数列{an}从第二项起,是以${a}_{2}=\frac{1}{3}$为首项,以$\frac{4}{3}$为公比的等比数列,则Sn可求.
解答 解:由Sn=3an+1,得
Sn-1=3an(n≥2),
两式作差得:an=3an+1-3an,即$\frac{{a}_{n+1}}{{a}_{n}}=\frac{4}{3}$(n≥2).
又a1=1,a1=S1=3a2,得${a}_{2}=\frac{1}{3}$.
∴数列{an}从第二项起,是以${a}_{2}=\frac{1}{3}$为首项,以$\frac{4}{3}$为公比的等比数列.
则S1=a1=1,当n≥2时,${S}_{n}=1+\frac{\frac{1}{3}[1-(\frac{4}{3})^{n-1}]}{1-\frac{4}{3}}=(\frac{4}{3})^{n-1}$.
已知S1适合上式,
∴${S}_{n}=(\frac{4}{3})^{n-1}$.
故答案为:${(\frac{4}{3})^{n-1}}$.
点评 本题考查数列递推式,考查了等比关系的确定,训练了等比数列前n项和公式的应用,是中档题.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
8.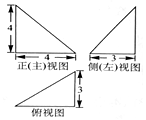 某四面体三视图如图所示,该四面体的体积为( )
某四面体三视图如图所示,该四面体的体积为( )
 某四面体三视图如图所示,该四面体的体积为( )
某四面体三视图如图所示,该四面体的体积为( )| A. | 8 | B. | 10 | C. | 20 | D. | 24 |
13.在△ABC中,三个内角A、B、C的对边分别是a,b,c,sinA>sinB则下列结论不一定成立的是( )
| A. | A>B | B. | sin2A>sin2B | C. | cos2A<cos2B | D. | a>b |
10.设变量x,y满足约束条件$\left\{\begin{array}{l}x-y≥0\\ 2x+y-2≤0\\ y+2≥0\end{array}\right.$,则目标函数z=|x+3y|的最大值为( )
| A. | 4 | B. | 6 | C. | 8 | D. | 10 |
13.已知向量$\overrightarrow{a}$=(sinx,cosx),$\overrightarrow{b}$=(sinx+cosx,sinx-cosx)(x∈R),若$\overrightarrow{a}$⊥$\overrightarrow{b}$,则x的取值集合为( )
| A. | {x|x=$\frac{kπ}{2}$+$\frac{π}{8}$,k∈Z} | B. | {x|x=kπ+$\frac{π}{8}$,k∈Z} | C. | {x|x=$\frac{kπ}{2}$+$\frac{π}{4}$,k∈Z} | D. | {x|x=kπ+$\frac{π}{4}$,k∈Z} |
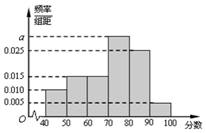 某校从高二年级学生中随机抽取60名学生,将其期中考试的政治成绩(均为整数)分成六段:[40,50),[50,60),…,[90,100]后得到如下频率分布直方图.
某校从高二年级学生中随机抽取60名学生,将其期中考试的政治成绩(均为整数)分成六段:[40,50),[50,60),…,[90,100]后得到如下频率分布直方图.