题目内容
20.小明家里有两双不同的拖鞋,求停电时他摸黑任穿2只恰好成双的概率( )| A. | $\frac{1}{6}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
分析 先求出基本事件总数n=${C}_{4}^{2}$=6,再求出恰好成双包含的基本事件个数,由此能求出停电时他摸黑任穿2只恰好成双的概率.
解答 解:小明家里有两双不同的拖鞋,停电时他摸黑任穿2只,
基本事件总数n=${C}_{4}^{2}$=6,
恰好成双包含的基本事件个数m=${C}_{2}^{2}+{C}_{2}^{2}$=2,
∴停电时他摸黑任穿2只恰好成双的概率p=$\frac{m}{n}$=$\frac{2}{6}=\frac{1}{3}$.
故选:C.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意等可能事件概率计算公式的合理运用.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
10.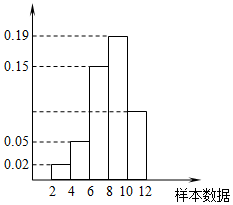 有一个容量为300的样本,其频率分布直方图如图所示.根据样本的频率分布直方图估计,样本数据落在区间[10,12)内的频数为( )
有一个容量为300的样本,其频率分布直方图如图所示.根据样本的频率分布直方图估计,样本数据落在区间[10,12)内的频数为( )
 有一个容量为300的样本,其频率分布直方图如图所示.根据样本的频率分布直方图估计,样本数据落在区间[10,12)内的频数为( )
有一个容量为300的样本,其频率分布直方图如图所示.根据样本的频率分布直方图估计,样本数据落在区间[10,12)内的频数为( )| A. | 27 | B. | 81 | C. | 54 | D. | 108 |
8.数$a={({\frac{1}{2}})^{0.1}},b={({\frac{1}{2}})^{-0.1}},c={({\frac{1}{2}})^{0.2}}$的大小关系是( )
| A. | a<b<c | B. | b<a<c | C. | c<a<b | D. | c<b<a |
9.袋中有大小相同的3个红球,5个白球,从中不放回地依次摸取2球,在已知第一次取出白球的前提下,第二次取得红球的概率是( )
| A. | $\frac{1}{5}$ | B. | $\frac{3}{10}$ | C. | $\frac{3}{8}$ | D. | $\frac{3}{7}$ |
