题目内容
10.实数m取何值时,复数z=m2(1+i)-(m+i)(1)是实数;
(2)是纯虚数;
(3)对应的点位于复平面的第一象限.
分析 复数z=m2(1+i)-(m+i)=m2-m+(m2-1)i.
(1)由m2-1=1,解得m即可得出.
(2)由$\left\{\begin{array}{l}{{m}^{2}-m=0}\\{{m}^{2}-1≠0}\end{array}\right.$,解得m,即可得出.
(3)由$\left\{\begin{array}{l}{{m}^{2}-m>0}\\{{m}^{2}-1>0}\end{array}\right.$,解得m即可得出.
解答 解:复数z=m2(1+i)-(m+i)=m2-m+(m2-1)i.
(1)由m2-1=1,解得m=±1.
∴m=±1时,复数z是实数.
(2)由$\left\{\begin{array}{l}{{m}^{2}-m=0}\\{{m}^{2}-1≠0}\end{array}\right.$,解得m=0,
∴m=0时,复数z是纯虚数.
(3)由$\left\{\begin{array}{l}{{m}^{2}-m>0}\\{{m}^{2}-1>0}\end{array}\right.$,解得m>1,或m<-1.
∴m>1,或m<-1时,对应的点位于复平面的第一象限.
点评 本题考查了复数的有关概念及其几何意义、方程的解法、不等式的解法,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
1.曲线y=$\frac{lnx-2x}{x}$在点(1,f(1))处的切线方程为( )
| A. | y=x-3 | B. | y=-x+1 | C. | y=2x-2 | D. | y=-2x+2 |
5.已知函数f(x)=$\left\{\begin{array}{l}{2^{-x}}-0.5,x≤1\\{log_{81}}x,x>1\end{array}$,则不等式f(x)>$\frac{1}{2}$的解集为( )
| A. | (-∞,1) | B. | (-∞,0)∪(9,+∞) | C. | (9,+∞) | D. | (-∞,1)∪(9,+∞) |
19.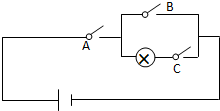 如图所示电路,有A、B、C三个开关,每个开关开或关的概率都是$\frac{1}{2}$,且相互独立,则灯泡亮的概率( )
如图所示电路,有A、B、C三个开关,每个开关开或关的概率都是$\frac{1}{2}$,且相互独立,则灯泡亮的概率( )
 如图所示电路,有A、B、C三个开关,每个开关开或关的概率都是$\frac{1}{2}$,且相互独立,则灯泡亮的概率( )
如图所示电路,有A、B、C三个开关,每个开关开或关的概率都是$\frac{1}{2}$,且相互独立,则灯泡亮的概率( )| A. | $\frac{1}{8}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{16}$ |