题目内容
已知向量
=(2,3),
=(x,y),x∈{0,1,2,3,4},y∈{-2,-1,1,2},则
⊥
的概率 .
| a |
| b |
| a |
| b |
考点:数量积判断两个平面向量的垂直关系,古典概型及其概率计算公式
专题:平面向量及应用,概率与统计
分析:先求出满足条件的向量
的个数,再求满足
⊥
的向量
的个数,由此能求出结果.
| b |
| a |
| b |
| b |
解答:
解:∵
=(x,y),x∈{0,1,2,3,4},y∈{-2,-1,1,2},
∴满足条件的向量
有5×4=20个,
∵
=(2,3),∴在这20个不同的向量中满足
⊥
的有:
=(3,-2),
∴
⊥
的概率p=
.
故答案为:
.
| b |
∴满足条件的向量
| b |
∵
| a |
| a |
| b |
| b |
∴
| a |
| b |
| 1 |
| 20 |
故答案为:
| 1 |
| 20 |
点评:本题考查概率的求法,是基础题,解题时要注意古典概型概率计算公式的灵活运用.

练习册系列答案
相关题目
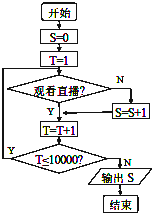 为了解“伦敦奥运会开幕式”电视直播节目的收视情况,某机构在某地随机抽查了10000人,把抽查结果输入如图所示的程序框图中,其输出的数值是3700,则该节目的收视率为( )
为了解“伦敦奥运会开幕式”电视直播节目的收视情况,某机构在某地随机抽查了10000人,把抽查结果输入如图所示的程序框图中,其输出的数值是3700,则该节目的收视率为( )| A、3700 | B、630 |
| C、0.63 | D、0.37 |