题目内容
10.有3个活动小组,甲、乙两位同学各自参加其中一个小组,每位同学参加各个小组的可能性相同,则这两位同学不在一个兴趣小组的概率为( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
分析 本题是一个古典概型,试验发生包含的事件数是3×3种结果,其中这两位同学参加同一个兴趣小组有3种结果,根据互斥事件的概率公式得到结果.
解答 解:由题意知本题是一个古典概型,
试验发生包含的事件数是3×3=9种结果,
其中这两位同学参加同一个兴趣小组,
由于共有三个小组,则有3种结果,
故这两位同学不在同一个兴趣小组的概率1-$\frac{3}{9}$=$\frac{2}{3}$,
故选:C
点评 本题主要考查相互独立事件的概率,等可能事件的概率,属于基础题.

练习册系列答案
相关题目
18.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一条渐近线平行于直线l:4x-3y+20=0,且双曲线的一个焦点在直线l上,则双曲线的方程为( )
| A. | $\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{16}$=1 | B. | $\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{9}$=1 | C. | $\frac{5{x}^{2}}{9}$-$\frac{5{y}^{2}}{16}$=1 | D. | $\frac{5{x}^{2}}{16}$-$\frac{5{y}^{2}}{9}$=1 |
5.已知$α∈[{π,\frac{3π}{2}}]$,$sinα=-\frac{3}{5}$,则tanα=( )
| A. | $-\frac{4}{3}$ | B. | $\frac{4}{3}$ | C. | $-\frac{3}{4}$ | D. | $\frac{3}{4}$ |
15.如果过点M(-2,0)的直线l与椭圆$\frac{x^2}{2}+{y^2}=1$有公共点,那么直线l的斜率k的取值范围是( )
| A. | $(-∞,-\frac{{\sqrt{2}}}{2}]$ | B. | $[\frac{{\sqrt{2}}}{2},+∞)$ | C. | $[-\frac{1}{2},\frac{1}{2}]$ | D. | $[-\frac{{\sqrt{2}}}{2},\frac{{\sqrt{2}}}{2}]$ |
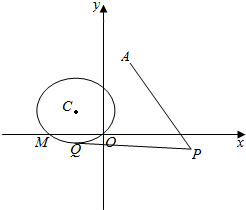 圆C过点M(-2,0)及原点,且圆心C在直线x+y=0上.
圆C过点M(-2,0)及原点,且圆心C在直线x+y=0上.