题目内容
18.如果执行如图的程序框图,那么输出的值是0.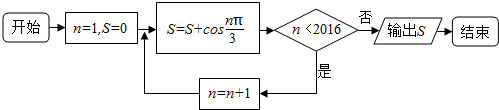
分析 由程序框图可得算法的功能是求S=cos$\frac{π}{3}$+cos$\frac{2π}{3}$+cosπ+…+cos$\frac{nπ}{3}$的值,根据条件判断跳出循环的n值,利用余弦函数的周期性求输出S的值.
解答 解:由程序框图知:算法的功能是求S=cos$\frac{π}{3}$+cos$\frac{2π}{3}$+cosπ+…+cos$\frac{nπ}{3}$的值,
∵跳出循环的n值为2016,
∴输出S=cos$\frac{π}{3}$+cos$\frac{2π}{3}$+cosπ+…+cos$\frac{2016π}{3}$,
又cos$\frac{nπ}{3}$+cos$\frac{(n+1)π}{3}$+cos$\frac{(n+2)π}{3}$+cos$\frac{(n+3)π}{3}$+cos$\frac{(n+4)π}{3}$+cos$\frac{(n+5)π}{3}$=0,
∴由2016=336×6,可得:S=cos$\frac{π}{3}$+cos$\frac{2π}{3}$+cosπ+…+cos$\frac{2016π}{3}$=0.
故答案为:-0
点评 本题考查了循环结构的程序框图,根据框图的流程判断算法的功能是关键,属于基础题.

练习册系列答案
 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
9.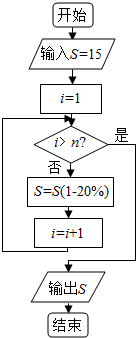 某人以15万元买了一辆汽车,此汽车将以每年20%的速度折旧,如图是描述汽车价值变化的算法流程图,则当n=4吋,最后输出的S的值为( )
某人以15万元买了一辆汽车,此汽车将以每年20%的速度折旧,如图是描述汽车价值变化的算法流程图,则当n=4吋,最后输出的S的值为( )
 某人以15万元买了一辆汽车,此汽车将以每年20%的速度折旧,如图是描述汽车价值变化的算法流程图,则当n=4吋,最后输出的S的值为( )
某人以15万元买了一辆汽车,此汽车将以每年20%的速度折旧,如图是描述汽车价值变化的算法流程图,则当n=4吋,最后输出的S的值为( )| A. | 9.6 | B. | 7.68 | C. | 6.144 | D. | 4.9152 |
13.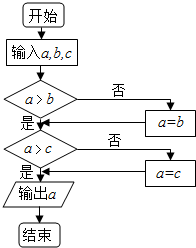 已知:a,b,c为集合A={1,2,3,4,5}中三个不同的数,通过如框图给出的一个算法输出一个整数a,则输出的数a=4的概率是( )
已知:a,b,c为集合A={1,2,3,4,5}中三个不同的数,通过如框图给出的一个算法输出一个整数a,则输出的数a=4的概率是( )
 已知:a,b,c为集合A={1,2,3,4,5}中三个不同的数,通过如框图给出的一个算法输出一个整数a,则输出的数a=4的概率是( )
已知:a,b,c为集合A={1,2,3,4,5}中三个不同的数,通过如框图给出的一个算法输出一个整数a,则输出的数a=4的概率是( )| A. | $\frac{3}{8}$ | B. | $\frac{3}{20}$ | C. | $\frac{3}{10}$ | D. | $\frac{1}{2}$ |
3.将4名同学录取到3所大学,则每所大学至少录取一名的概率为( )
| A. | $\frac{4}{27}$ | B. | $\frac{8}{27}$ | C. | $\frac{4}{9}$ | D. | $\frac{8}{9}$ |
10.“x为无理数”是“x2为无理数”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
7.设 a=${(\frac{1}{3})^{0.2}},b={2^{\frac{1}{3}}}$,则a,b 的大小关系是( )
| A. | a>b | B. | a<b | C. | a=b | D. | 不能确定 |