题目内容
设z=2x+5y,其中实数x,y满足6≤x+y≤8且-2≤x-y≤0,则z的最大值是( )
| A、21 | B、24 | C、28 | D、31 |
考点:简单线性规划
专题:不等式的解法及应用
分析:作出不等式组对应的平面区域,利用z的几何意义进行求解即可.
解答:
 解:作出不等式组对应的平面区域如图:
解:作出不等式组对应的平面区域如图:
由z=2x+5y,得y=-
x+
表示,
平移直线y=-
x+
,当直线y=-
x+
经过点A时,直线y=-
x+
的截距最大,此时z最大,
由
得
,即A(3,5),此时zmax=2×3+5×5=31.
故选:D.
 解:作出不等式组对应的平面区域如图:
解:作出不等式组对应的平面区域如图:由z=2x+5y,得y=-
| 2 |
| 5 |
| z |
| 5 |
平移直线y=-
| 2 |
| 5 |
| z |
| 5 |
| 2 |
| 5 |
| z |
| 5 |
| 2 |
| 5 |
| z |
| 5 |
由
|
|
故选:D.
点评:本题主要考查线性规划的基本应用,利用z的几何意义是解决线性规划问题的关键,注意利用数形结合来解决.

练习册系列答案
相关题目
若函数f(x)=
f′(-1)x2-2x+3,则f′(-1)的值为( )
| 1 |
| 2 |
| A、0 | B、-1 | C、1 | D、2 |
复数z=(m-1)(m-8)+
ilog2m(m∈R)是纯虚数,则
=( )
| 1 |
| 3 |
| 1 |
| 1-z |
| A、1+i | ||||
| B、1-i | ||||
C、
| ||||
D、
|
已知复数z满足
=i(其中i是虚数单位),则z为( )
| z+2 |
| z-2 |
| A、2i | B、-2i | C、i | D、-i |
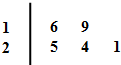 学校为了了解学生每个月在校期间参加体育锻炼的时间,从某班选取5名学生进行调查,他们参加体育锻炼的时间用茎叶图记录如图所示(单位:小时),则这组数据的中位数和方差分别是( )
学校为了了解学生每个月在校期间参加体育锻炼的时间,从某班选取5名学生进行调查,他们参加体育锻炼的时间用茎叶图记录如图所示(单位:小时),则这组数据的中位数和方差分别是( )| A、21和10.8 |
| B、24和10.8 |
| C、25和9.2 |
| D、5和9.2 |
C的方程为(x-1)2+(y-2)2=4,则圆C的圆心坐标和半径r分别为( )
| A、(1,2),r=2 |
| B、(-1,-2),r=2 |
| C、(1,2),r=4 |
| D、(-1,-2),r=4 |
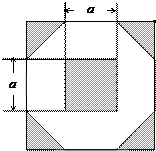 为增加绿化面积,某小区将原来正方形地砖更换为如图所示的正八边形植草砖,更换后,图中阴影部分为植草区域,设正八边形与其内部小正方形的边长都为a,则阴影部分的面积为( )
为增加绿化面积,某小区将原来正方形地砖更换为如图所示的正八边形植草砖,更换后,图中阴影部分为植草区域,设正八边形与其内部小正方形的边长都为a,则阴影部分的面积为( )| A、2a2 |
| B、3a2 |
| C、4a2 |
| D、5a2 |