题目内容
sin75°•sin15°的值是（ ）
A、
| ||||
B、
| ||||
C、
| ||||
| D、0 |
考点：二倍角的正弦
专题：三角函数的求值
分析：利用诱导公式把要求的式子化为cos15°sin15°，再利用二倍角的正弦公式求得它的值．
解答：
解：sin75°•sin15°=cos15°sin15°=
sin30°=
，
故选：A．
| 1 |
| 2 |
| 1 |
| 4 |
故选：A．
点评：本题主要考查诱导公式、二倍角的正弦公式的应用，属于基础题．
练习册系列答案
相关题目
在△ABC中，
•
=7，|
-
|=6，则△ABC面积的最大值为（ ）
| AB |
| AC |
| AB |
| AC |
| A、24 | B、16 | C、12 | D、8 |
已知函数f（x）=
sinx+
cosx在x0处取得最大值，则x0可能是（ ）
| ||
| 2 |
| 1 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知角θ的顶点与原点重合，始边与x轴的正半轴重合，终边过x=1与曲线y=2x的交点，则cos2θ=（ ）
A、-
| ||
B、
| ||
C、-
| ||
D、
|
“k=-1”是“两直线kx+3y-2=0和（2-k）x+y-7=0互相垂直”的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分又不必要条件 |
已知角α的终边过点P（x，-3）且cosα=-
，则x的值为（ ）
| ||
| 2 |
A、±3
| ||||
B、3
| ||||
C、-3
| ||||
D、-
|
已知△ABC中，tanA=-
，那么cosA等于（ ）
| 5 |
| 12 |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
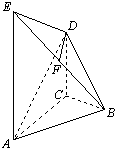在如图所示的几何体中，AE⊥平面ABC，CD∥AE，F是BE的中点，AC=BC=1，∠ACB=90°，AE=2CD=2．