题目内容
18.在△ABC中,内角A,B,C的时边分别为a,b,c,△ABC的面积记为S,若acosB+bcosA=c•sinC,且S=$\frac{1}{4}$(b2+c2-a2),则角B=$\frac{π}{4}$.分析 acosB+bcosA=c•sinC,正弦定理化为sin(A+B)=sinC=sinCsinC,由于C∈(0,π),可得sinC=1,解得C.由S=$\frac{1}{4}$(b2+c2-a2),利用三角形面积及其余弦定理可得:$\frac{1}{2}$bcsinA=$\frac{1}{4}$•2bccosA,化简即可得出.
解答 解:∵acosB+bcosA=c•sinC,∴sinAcosB+sinBcosA=sinC•sinC,化为sin(A+B)=sinC=sinCsinC,
∵C∈(0,π),∴sinC≠0,∴sinC=1,解得C=$\frac{π}{2}$.
∵S=$\frac{1}{4}$(b2+c2-a2),∴$\frac{1}{2}$bcsinA=$\frac{1}{4}$•2bccosA,化为tanA=1,又A为锐角,∴A=$\frac{π}{4}$.
故答案为:$\frac{π}{4}$.
点评 本题考查了和差公式、三角形内角和定理、正弦定理、余弦定理、三角函数的单调性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.函数y=sin($\frac{1}{2}$x+θ)是偶函数,则θ的一个值是( )
| A. | -π | B. | -$\frac{π}{2}$ | C. | -$\frac{π}{4}$ | D. | -$\frac{π}{8}$ |
 如图,在直角坐标系xOy中,已知圆O:x2+y2=4.点B,C在圆O上,且关于x轴对称.
如图,在直角坐标系xOy中,已知圆O:x2+y2=4.点B,C在圆O上,且关于x轴对称.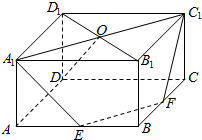 如图.在直四棱柱ABCD-A1B1C1D1中,E,F分別AB,BC的中点,A1C1与B1D1交于点O.
如图.在直四棱柱ABCD-A1B1C1D1中,E,F分別AB,BC的中点,A1C1与B1D1交于点O.