题目内容

12．已知函数f（x）=x3+ax2+bx在x=1处取极值10，则b-a=21．

分析 首先对f（x）求导，然后由题设在x=1时有极值10可得，f′（1）=0，f（1）=10．，解之即可求出a和b的值．

解答 解：对函数函数f（x）=x3+ax2+bx，求导得 f′（x）=3x2+2ax+b，
又∵在x=1处取极值10，
∴f′（1）=3+2a+b=0，f（1）=1+a+b=10，
解得，a=-6，b=15，
b-a=21．
故答案为：21．

点评 本题考查掌握函数极值存在的条件，利用函数的极值存在的条件求参数的能力，属于中档题．

练习册系列答案
相关题目
2．我省某校要进行一次月考，一般考生必须考5 门学科，其中语、数、英、综合这四科是必考科目，另外一门在物理、化学、政治、历史、生物、地理、英语Ⅱ中选择．为节省时间，决定每天上午考两门，下午考一门学科，三天半考完．
（1）若语、数、英、综合四门学科安排在上午第一场考试，则“考试日程安排表”有多少种不同的安排方法；
（2）如果各科考试顺序不受限制，求数学、化学在同一天考的概率是多少？
3．如图，己知平行四边形ABCD中，∠BAD=60°，AB=6，AD=3，G为CD中点，现将梯形ABCG沿着AG折起到AFEG．
（I）求证：直线CE∥平面ABF；
（II）如果FG⊥平面ABCD求二面B一EF一A的平面角的余弦值．
（Ⅲ）若直线AF与平面 ABCD所成角为$\frac{π}{6}$，求证：FG⊥平面ABCD
20．已知点A（-1，0），B（1，0），△ABC的周长为6．
（Ⅰ）求动点C的轨迹E的方程；
（Ⅱ）设过点B（1，0）的直线l与曲线E相交于不同的两点M，N．若点P在y轴上，且|PM|=|PN|，求点P的纵坐标的取值范围．
7．已知向量$\overrightarrow{a}$与向量$\overrightarrow{b}$的夹角为120°，若向量$\overrightarrow{c}=\overrightarrow{a}+\overrightarrow{b}$，且$\overrightarrow{a}⊥\overrightarrow{c}$，则$\frac{|\overrightarrow{a}|}{|\overrightarrow{b}|}$的值为（　　）
A．$\frac{1}{2}$B．$\frac{2\sqrt{3}}{3}$C．2D．$\sqrt{3}$
17．已知圆O：x2+y2=1，圆O关于直线x+y+2=0对称的圆C．
（1）求圆C的方程；
（2）在直线l：2x+y-3=0上是否存在点P，过点P分别作圆O，圆C的两条切线PA，PB分别为A，B，有PA=PB？若存在，求出点P的坐标，若不存在说明理由．
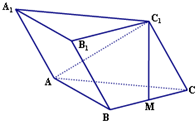4．如图，斜三棱柱ABC-A1B1C1的所有棱长均为a，M是BC的中点，侧面B1C1CB⊥底面ABC，且AC1⊥BC．
（Ⅰ）求证：BC⊥C1M；
（Ⅱ）求二面角A1-AB-C的平面角的余弦值．
1．已知函数f（x）=lnx-a（x-1），g（x）=ex，其中e为自然对数的底数．
（Ⅰ）设$t（x）=\frac{1}{x}g（x），x∈（0，+∞）$，求函数t（x）在[m，m+1]（m＞0）上的最小值；
（Ⅱ）过原点分别作曲线y=f（x）与y=g（x）的切线l1，l2，已知两切线的斜率互为倒数，
求证：a=0或$\frac{e-1}{e}＜a＜\frac{{{e^2}-1}}{e}$．
2．f（x）=$\left\{{\begin{array}{l}{\frac{1}{x}+alnx，（x＞0，0＜a＜e）}\\{cosx，（x≤0）}\end{array}}$，则y=f[f（x）]的零点有（　　）
A．0个B．1个C．2个D．无穷多个

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网