题目内容
10.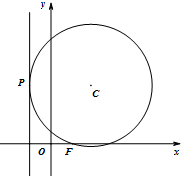 如图,动圆C过点F(1,0),且与直线x=-1相切于点P.
如图,动圆C过点F(1,0),且与直线x=-1相切于点P.(Ⅰ)求圆心C的轨迹Γ的方程;
(Ⅱ)过点F任作一直线交轨迹Γ于A,B两点,设PA,PF,PB的斜率分别为k1,k2,k3,问:$\frac{{{k_1}+{k_3}}}{k_2}$是否为定值?若是,求出此定值;若不是,请说明理由.
分析 (Ⅰ)利用抛物线的定义,求圆心C的轨迹Γ的方程;
(Ⅱ)设直线AB的方程为x=my+1,与抛物线方程联立,可得y2-4my-4=0,设A(x1,y1),B(x2,y2),得到根与系数的关系,即可得出结论.
解答 解:(Ⅰ)由题意,圆心C到点F的距离与到直线x=-1的距离相等,
由抛物线的定义,可得,圆心C的轨迹是以F 为焦点,x=-1为准线的抛物线,
∴圆心C的轨迹Γ的方程为y2=4x;
(Ⅱ)设直线AB的方程为x=my+1,与抛物线方程联立,可得y2-4my-4=0
设A(x1,y1),B(x2,y2),则y1+y2=4m,y1y2=-4
设P(-1,t),则k1=$\frac{{y}_{1}-t}{m{y}_{1}+2}$,k3=$\frac{{y}_{2}-t}{m{y}_{2}+2}$,k2=-$\frac{t}{2}$,
∴k1+k3=$\frac{{y}_{1}-t}{m{y}_{1}+2}$+$\frac{{y}_{2}-t}{m{y}_{2}+2}$=-t=2k2,
∴$\frac{{{k_1}+{k_3}}}{k_2}$=2为定值.
点评 本题考查了抛物线的定义及其性质、直线与抛物线的位置关系,考查斜率的计算,考查了分析问题与解决问题的能力,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
18.某三棱锥的三视图如图所示,其中左视图中虚线平分底边,则该三棱锥的所有面中最大面的面积是( )
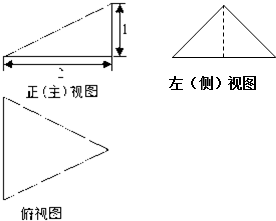

| A. | 2 | B. | $\sqrt{5}$ | C. | 2$\sqrt{5}$ | D. | $\frac{{\sqrt{5}}}{2}$ |
2.f(x)=$\left\{{\begin{array}{l}{\frac{1}{x}+alnx,(x>0,0<a<e)}\\{cosx,(x≤0)}\end{array}}$,则y=f[f(x)]的零点有( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 无穷多个 |
19.设实数x,y满足$\left\{\begin{array}{l}2x-y≥0\\ x+y-3≥0\\ y-x≥0\end{array}\right.$,则z=2x+y的最小值为( )
| A. | $\frac{9}{2}$ | B. | 4 | C. | 3 | D. | 0 |
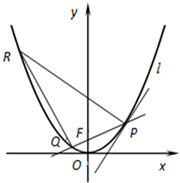 如图,点F是抛物线C:x2=2y的焦点,点P(x1,y1)为抛物线上的动点(P在第一象限),直线PF交抛物线C于另一点Q,直线l与抛物线C相切于点P.过点P作直线l的垂线交抛物线C于点R.
如图,点F是抛物线C:x2=2y的焦点,点P(x1,y1)为抛物线上的动点(P在第一象限),直线PF交抛物线C于另一点Q,直线l与抛物线C相切于点P.过点P作直线l的垂线交抛物线C于点R.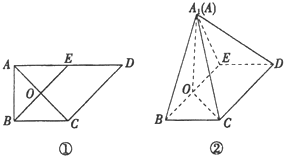 如图①,在直角梯形ABCD中,AD∥BC,∠BAD=$\frac{π}{2}$,AB=BC=$\sqrt{2}$,AD=2$\sqrt{2}$,E是AD的中点,O是AC与BE的交点.将△ABE沿BE折起到△A1BE的位置,如图②.
如图①,在直角梯形ABCD中,AD∥BC,∠BAD=$\frac{π}{2}$,AB=BC=$\sqrt{2}$,AD=2$\sqrt{2}$,E是AD的中点,O是AC与BE的交点.将△ABE沿BE折起到△A1BE的位置,如图②.