题目内容
17．在三棱锥P-ABC中，AB⊥BC，AB=BC=$\sqrt{2}$，PA=PC=2，AC中点为M，cos∠PMB=$\frac{{\sqrt{3}}}{3}$，则此三棱锥的外接球的表面积为（ ）| A． | $\frac{3π}{2}$ | B． | 2π | C． | 6π | D． | $\sqrt{6}$π |
分析 利用条件，判断AB，PB，BC互相垂直，可得三棱锥的外接球的直径，即可求出三棱锥的外接球的表面积．
解答 解：由题意，AC=2，BM=1，PM=$\sqrt{3}$，
∵cos∠PMB=$\frac{{\sqrt{3}}}{3}$，∴PB=$\sqrt{2}$，
∴AB，PB，BC互相垂直，
∴三棱锥的外接球的直径为$\sqrt{6}$，
∴三棱锥的外接球的表面积为$4π•（\frac{\sqrt{6}}{2}）^{2}$=6π，
故选C．
点评 本题考查三棱锥的外接球的表面积，考查学生的计算能力，正确求出三棱锥的外接球的直径是关键．
练习册系列答案
名师指导期末冲刺卷系列答案
开心蛙口算题卡系列答案
相关题目
7．已知向量$\overrightarrow{a}$与向量$\overrightarrow{b}$的夹角为120°，若向量$\overrightarrow{c}=\overrightarrow{a}+\overrightarrow{b}$，且$\overrightarrow{a}⊥\overrightarrow{c}$，则$\frac{|\overrightarrow{a}|}{|\overrightarrow{b}|}$的值为（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{2\sqrt{3}}{3}$ | C． | 2 | D． | $\sqrt{3}$ |
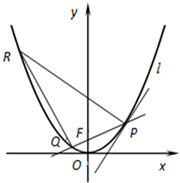如图，点F是抛物线C：x2=2y的焦点，点P（x1，y1）为抛物线上的动点（P在第一象限），直线PF交抛物线C于另一点Q，直线l与抛物线C相切于点P．过点P作直线l的垂线交抛物线C于点R．